Physics:Ideal surface

An ideal solid surface is flat, rigid, perfectly smooth, and chemically homogeneous, and has zero contact angle hysteresis. Zero hysteresis implies the advancing and receding contact angles are equal.

Figure 1: Contact angle for a liquid droplet on a solid surface

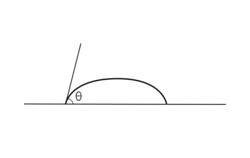
In other words, only one thermodynamically stable contact angle exists. When a drop of liquid is placed on such a surface, the characteristic contact angle is formed as depicted in Fig. 1. Furthermore, on an ideal surface, the drop will return to its original shape if it is disturbed. The following derivations apply only to ideal solid surfaces; they are only valid for the state in which the interfaces are not moving and the phase boundary line exists in equilibrium.

Figure 2: Wetting of different fluids: A shows a fluid with very little wetting, while C shows a fluid with more wetting. A has a large contact angle, and C has a small contact angle.

Minimization of energy, three phases

Figure 3: Coexistence of three fluid phases in mutual contact: α, β, and θ represent both the labels of the phases and the contact angles.

Figure 4: Neumann's triangle relating the surface energies and contact angles of three fluid phases coexisting in static equilibrium, as depicted in Figure 3

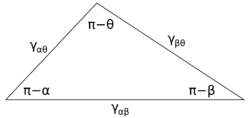
Figure 3 shows the line of contact where three phases meet. In equilibrium, the net force per unit length acting along the boundary line between the three phases must be zero. The components of net force in the direction along each of the interfaces are given by:

[math]\displaystyle{ \gamma_{\alpha\theta}+\gamma_{\theta\beta}\cos{\theta}+\gamma_{\alpha\beta}\cos{\alpha}\ = 0 }[/math]

[math]\displaystyle{ \gamma_{\alpha\theta}\cos{\theta}+\gamma_{\theta\beta}+\gamma_{\alpha\beta}\cos{\beta}\ = 0 }[/math]

[math]\displaystyle{ \gamma_{\alpha\theta}\cos{\alpha}+\gamma_{\theta\beta}\cos{\beta}+\gamma_{\alpha\beta}\ = 0 }[/math]

where α, β, and θ are the angles shown and γ_ij is the surface energy between the two indicated phases. These relations can also be expressed by an analog to a triangle known as Neumann’s triangle, shown in Figure 4. Neumann’s triangle is consistent with the geometrical restriction that [math]\displaystyle{ \alpha+\beta+\theta=2\pi }[/math], and applying the law of sines and law of cosines to it produce relations that describe how the interfacial angles depend on the ratios of surface energies.

Because these three surface energies form the sides of a triangle, they are constrained by the triangle inequalities, γ_ij < γ_jk + γ_ik meaning that no one of the surface tensions can exceed the sum of the other two. If three fluids with surface energies that do not follow these inequalities are brought into contact, no equilibrium configuration consistent with Figure 3 will exist.

Simplification to planar geometry, Young's relation

If the β phase is replaced by a flat rigid surface, as shown in Figure 5, then β = π, and the second net force equation simplifies to the Young equation,

Figure 5: Contact angle of a liquid droplet wetted to a rigid solid surface

[math]\displaystyle{ \gamma_{SG}\ =\gamma_{SL}+\gamma_{LG}\cos{\theta} }[/math]

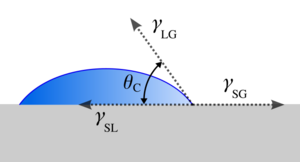
which relates the surface tensions between the three phases: solid, liquid and gas. Subsequently, this predicts the contact angle of a liquid droplet on a solid surface from knowledge of the three surface energies involved. This equation also applies if the "gas" phase is another liquid, immiscible with the droplet of the first "liquid" phase.

Real smooth surfaces and the Young contact angle

The Young equation assumes a perfectly flat and rigid surface. In many cases, surfaces are far from this ideal situation, and two are considered here: the case of rough surfaces and the case of smooth surfaces that are still real (finitely rigid). Even in a perfectly smooth surface, a drop will assume a wide spectrum of contact angles ranging from the so-called advancing contact angle, [math]\displaystyle{ \theta_\mathrm{A} }[/math], to the so-called receding contact angle, [math]\displaystyle{ \theta_\mathrm{R} }[/math]. The equilibrium contact angle ([math]\displaystyle{ \theta_\mathrm{c} }[/math]) can be calculated from [math]\displaystyle{ \theta_\mathrm{A} }[/math] and [math]\displaystyle{ \theta_\mathrm{R} }[/math] as was shown by Tadmor as,

[math]\displaystyle{ \theta_\mathrm{c}=\arccos\left(\frac{r_\mathrm{A}\cos{\theta_\mathrm{A}}+r_\mathrm{R}\cos{\theta_\mathrm{R}}}{r_\mathrm{A}+r_\mathrm{R}}\right) }[/math]

where

[math]\displaystyle{ r_\mathrm{A}=\left(\frac{\sin^3{\theta_\mathrm{A}}}{2-3\cos{\theta_\mathrm{A}}+\cos^3{\theta_\mathrm{A}}}\right)^{1/3} ~;~~ r_\mathrm{R}=\left(\frac{\sin^3{\theta_\mathrm{R}}}{2-3\cos{\theta_\mathrm{R}}+\cos^3{\theta_\mathrm{R}}}\right)^{1/3} }[/math]

The Young–Dupré equation and spreading coefficient

The Young–Dupré equation (Thomas Young 1805, Lewis Dupré 1855) dictates that neither γ_SG nor γ_SL can be larger than the sum of the other two surface energies. The consequence of this restriction is the prediction of complete wetting when γ_SG > γ_SL + γ_LG and zero wetting when γ_SL > γ_SG + γ_LG. The lack of a solution to the Young–Dupré equation is an indicator that there is no equilibrium configuration with a contact angle between 0 and 180° for those situations.

A useful parameter for gauging wetting is the spreading parameter S,

[math]\displaystyle{ S\ = \gamma_{SG}-(\gamma_{SL}+\gamma_{LG}) }[/math]

When S > 0, the liquid wets the surface completely (complete wetting). When S < 0, partial wetting occurs.

Combining the spreading parameter definition with the Young relation yields the Young–Dupré equation:

[math]\displaystyle{ S\ = \gamma_{LG}(\cos\theta-1) }[/math]

which only has physical solutions for θ when S < 0.

See also

• Contact angle
• hysteresis
• Wetting
• Surface roughness

External links

• The effect of surface roughness to contact angle