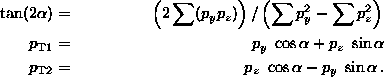Physics:Jet variables

In many collisions, observable secondary particles are produced in highly collimated form, called particle jets. This is a consequence of the hadronization of partons (quarks or gluons) produced in hard collisions. Jets for a given initial parton can vary widely in shape, particle content, and energy spectrum; there is, of course, also substantial blurring due to instrumental effects: the finite resolution and granularity of detectors (calorimeter cells and muon measurements), and escaping neutrinos.

The earliest evidence for jets was in e⁺e^- collisions (SLAC and DESY), producing secondary hadrons; subsequently, they were also observed in hadronic collisions (e.g. UA experiments and ISR at CERN). Frequently, two main jets are observed which dominate the energy balance of the collision; in hadronic collider events, the balance is observed only laterally, due to the difficulty of observing at large (absolute) rapidity, and due to the structure function, which leaves the hard quark encounter with a longitudinal boost. Often, the main jets are accompanied by one or more broader jet(s), interpreted as radiated gluons. The following scalar jet variables were used in the early jet studies, describing mostly a two- or three-jet situation from e⁺e^- events.

• a) Sphericity
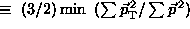
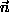  is the transverse momentum perpendicular to a unit vector , the sums are over all particles of the reaction, and the minimum is formed with respect to .
• b) Thrust
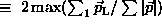
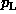  is the longitudinal momentum along a unit vector 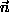. Summation is over all particles for |p|, over those with 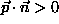for 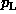 ; the maximum is formed with respect to 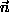. For the hadronic system in deep inelastic scattering, a current thrust has been proposed (see Webber95) which is the thrust evaluated in the Breit frame , defined to be the frame in which the momentum transfer q is spacelike and along the longitudinal (z-) axis ( Deep Inelastic Scattering Variables).
• c) Spherocity (4/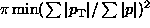
  is the transverse momentum perpendicular to a unit vector 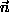, the sums are over all particles, and the minimization is with respect to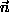
• d) Triplicity
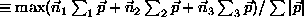
  Here, a general classification into three classes must take place; in each class i,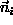 describes the axis and particles are associated to the class for which 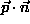is largest. The maximum must be found over all possible .

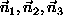• e) Planarity
  Here, and are defined to be axes of a Cartesian coordinate system whose third axis is 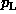. The variable indicates how well a reaction satisfies the assumption of being in a plane. The maximum is found with respect to the plane orientation. Maximization gives the same result if 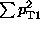is maximized. The solution is therefore given by the principal axes (obtained in ``principal component analysis), and the planarity is the complement of a two-dimensional equivalent to sphericity (called circularity). If 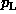is along x, then the direction for is obtained by rotating in the y-z plane through an angle 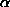given by

  

  As maxima and minima differ by 90 in 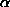, solving the above equation for an 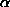in the range, say, from 0 to /2, will still require deciding whether a maximum or minimum has been found. Obviously, .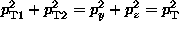

  The variables a) to c) all describe two-jet situations, with the jets back to back ( 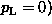. d) has been used for a general three-jet situation. A detailed discussion of these variables can be found in Brandt79. The planarity e) describes a four-jet situation, if pairs of jets are correlated, e.g. a hard-scattered and a spectator system. The scattered system may have 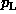different from zero, but will be in a plane with the spectator jets and back to back in the transverse projection. A more recent discussion on e⁺e^--produced jets can also be found in Akrawy90.

  Jets are not well-defined phenomena, hadrons in the final state not being rigorously associated to the partons (which in turn also undergo some final-state interactions before they hadronize). In hadron-hadron collisions, jets are particularly difficult to separate: there is an underlying event due to the remnants from the quarks not participating in the hard interaction, and at high luminosity, there may be pileup of multiple collisions that cannot be separated in time (e.g. at the planned Large Hadron Collider).

  In jet analysis of more recent dates, therefore, simple jet variables have been somewhat abandoned; jets are analysed in cones defined by a cutoff (typically between 0.5 and 1.0) in an angular radius 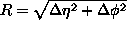around a jet axis defined in various ways. Jets thus found are often subsequently contracted, viz. combined into fewer jets, using some clustering algorithm.

  The jet structure is studied as a function of the jet radius; particle multiplicities, rapidity distributions, fragmentation functions, and others (and again their gradients, when varying the cone radius) are eventually compared to the values obtained from phenomenological Monte Carlo programs; e.g. Ellis91, Bethke91, Buskulic96, Varelas96.

  Some specific variables are used for multijet events: in three-jet events, labelling the outgoing jets 3, 4, 5 after ordering them by decreasing energy (jet 3 is thus the highest-energy or leading jet),

  one uses

• f) the Dalitz variables:

  

  with M the three-jet effective mass;

• g) the scattering angle of the leading jet:

  

• h) the angle in the three-jet rest frame between the plane containing the leading jet and the beam, and the three-jet plane:

  

In these formulae, , refers to the effective parton beam, i.e. the difference between the momenta of the colliding partons. For higher jet multiplicities, one often uses variables reducing to three jets. For details and results, e.g. Abe92, Acton93.