Physics:Kibble–Zurek mechanism

The Kibble–Zurek mechanism (KZM) describes the non-equilibrium dynamics and the formation of topological defects in a system which is driven through a continuous phase transition at finite rate. It is named after Tom W. B. Kibble, who pioneered the study of domain structure formation through cosmological phase transitions in the early universe, and Wojciech H. Zurek, who related the number of defects it creates to the critical exponents of the transition and to its rate—to how quickly the critical point is traversed.

Basic idea

Based on the formalism of spontaneous symmetry breaking, Tom Kibble developed the idea for the primordial fluctuations of a two-component scalar field like the Higgs field. If a two-component scalar field switches from the isotropic and homogeneous high-temperature phase to the symmetry-broken stage during cooling and expansion of the very early universe (shortly after Big Bang), the order parameter necessarily cannot be the same in regions which are not connected by causality. Regions are not connected by causality if they are separated far enough (at the given age of the universe) that they cannot "communicate" even with the speed of light. This implies that the symmetry cannot be broken globally. The order parameter will take different values in causally disconnected regions, and the domains will be separated by domain walls after further evolution of the universe. Depending on the symmetry of the system and the symmetry of the order parameter, different types of topological defects like monopoles, vortices or textures can arise. It was debated for quite a while if magnetic monopoles might be residuals of defects in the symmetry-broken Higgs field. Up to now, defects like this have not been observed within the event horizon of the visible universe. This is one of the main reasons (beside the isotropy of the cosmic background radiation and the flatness of spacetime) why nowadays an inflationary expansion of the universe is postulated. During the exponentially fast expansion within the first 10⁻³⁰ second after Big-Bang, all possible defects were diluted so strongly that they lie beyond the event horizon. Today, the two-component primordial scalar field is usually named inflaton.

Relevance in condensed matter

The blue curve shows the divergence of correlation times as function of the control parameter (e.g. temperature difference to the transition). The red curve indicates the time to reach the transition as function of the control parameter for linear cooling rates. The intersection point marks the temperature/time when the system falls out of equilibrium and gets non-adiabatic.

Wojciech Zurek pointed out, that the same ideas play a role for the phase transition of normal fluid helium to superfluid helium. The analogy between the Higgs field and superfluid helium is given by the two-component order parameter; superfluid helium is described via a macroscopic quantum mechanical wave function with global phase. In helium, two components of the order parameter are magnitude and phase (or real and imaginary part) of the complex wave function. Defects in superfluid helium are given by vortex lines, where the coherent macroscopic wave function disappears within the core. Those lines are high-symmetry residuals within the symmetry broken phase.

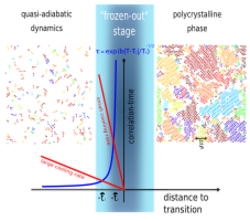
It is characteristic for a continuous phase transition that the energy difference between ordered and disordered phase disappears at the transition point. This implies that fluctuations between both phases will become arbitrarily large. Not only the spatial correlation lengths diverge for those critical phenomena, but fluctuations between both phases also become arbitrarily slow in time, described by the divergence of the relaxation time. If a system is cooled at any non-zero rate (e.g. linearly) through a continuous phase transition, the time to reach the transition will eventually become shorter than the correlation time of the critical fluctuations. At this time, the fluctuations are too slow to follow the cooling rate; the system has fallen out of equilibrium and ceases to be adiabatic. A "fingerprint" of critical fluctuations is taken at this fall-out time and the longest-length scale of the domain size is frozen out. The further evolution of the system is now determined by this length scale. For very fast cooling rates, the system will fall out of equilibrium very early and far away from the transition. The domain size will be small. For very slow rates, the system will fall out of equilibrium in the vicinity of the transition when the length scale of critical fluctuations will be large, thus the domain size will be large, too. The inverse of this length scale can be used as an estimate of the density of topological defects, and it obeys a power law in the quench rate. This prediction is universal, and the power exponent is given in terms of the critical exponents of the transition.

Derivation of the defect density

Exponential divergence of correlation times of a Kosterlitz–Thouless transition. Left inset shows the domain structure of a 2D colloidal mono-layer for large cooling rates at the fall-out time. The right inset shows the structure for small cooling rates (after additional coarsening) a late times.

Domain size as function of cooling rate in a colloidal mono-layer. The control parameter is given by the interaction strength [math]\displaystyle{ \Gamma }[/math] in this system.

Consider a system that undergoes a continuous phase transition at the critical value [math]\displaystyle{ \lambda = \lambda_c = 0 }[/math] of a control parameter. The theory of critical phenomena states that, as the control parameter is tuned closer and closer to its critical value, the correlation length [math]\displaystyle{ \xi }[/math] and the relaxation time [math]\displaystyle{ \tau }[/math] of the system tend to diverge algebraically with the critical exponent [math]\displaystyle{ \nu }[/math] as [math]\displaystyle{ \xi \sim \lambda^{-\nu}, \qquad \tau \sim \lambda^{-z\nu}, }[/math] respectively. [math]\displaystyle{ z }[/math] is the dynamic exponent which relates spatial with temporal critical fluctuations.

The Kibble–Zurek mechanism describes the nonadiabatic dynamics resulting from driving a high-symmetry (i.e. disordered) phase [math]\displaystyle{ \lambda\ll0 }[/math] to a broken-symmetry (i.e. ordered) phase at [math]\displaystyle{ \lambda\gg0 }[/math]. If the control parameter varies linearly in time, [math]\displaystyle{ \lambda(t) = vt }[/math], equating the time to the critical point to the relaxation time, we obtain the freeze out time [math]\displaystyle{ \bar{t} }[/math], [math]\displaystyle{ \bar{t} = [\lambda(\bar{t})]^{-z\nu} \Rightarrow \bar{t} \sim v^{-z\nu / (1+z\nu)}. }[/math] This time scale is often referred to as the freeze-out time. It is the intersection point of the blue and the red curve in the figure. The distance to the transition is on one hand side the time to reach the transition as function of cooling rate (red curve) and for linear cooling rates at the same time the difference of the control parameter to the critical point (blue curve). As the system approaches the critical point, it freezes as a result of the critical slowing down and falls out of equilibrium. Adiabaticity is lost around [math]\displaystyle{ -\bar{t} }[/math]. Adiabaticity is restored in the broken-symmetry phase after [math]\displaystyle{ +\bar{t} }[/math]. The correlation length at this time provides a length scale for coherent domains, [math]\displaystyle{ \bar{\xi} \equiv \xi[\lambda(\bar{t})] \sim v^{-\nu/(1+z\nu)}. }[/math] The size of the domains in the broken-symmetry phase is set by [math]\displaystyle{ \bar{\xi} }[/math]. The density of defects immediately follows if [math]\displaystyle{ d }[/math] is the dimension of the system, using [math]\displaystyle{ \rho \sim \bar{\xi}^{-d}. }[/math]

Experimental tests

The Kibble–Zurek mechanism generally applies to spontaneous symmetry breaking scenarios where a global symmetry is broken. For gauge symmetries defect formation can arise through the Kibble–Zurek mechanism and the flux trapping mechanism proposed by Hindmarsh and Rajantie. In 2005, it was shown that KZM describes as well the dynamics through a quantum phase transition.

The mechanism also applies in the presence of inhomogeneities, ubiquitous in condensed matter experiments, to both classical, quantum phase transitions and even in optics. A variety of experiments have been reported that can be described by the Kibble–Zurek mechanism. A review by T. Kibble discusses the significance and limitations of various experiments (until 2007).

Example in two dimensions

A system, where structure formation can be visualized directly is given by a colloidal mono-layer which forms a hexagonal crystal in two dimensions. The phase transition is described by the so-called Kosterlitz–Thouless–Halperin–Nelson–Young theory where translational and orientational symmetry are broken by two Kosterlitz–Thouless transitions. The corresponding topological defects are dislocations and disclinations in two dimensions. The latter are nothing else but the monopoles of the high-symmetry phase within the six-fold director field of crystal axes. A special feature of Kosterlitz–Thouless transitions is the exponential divergence of correlation times and length (instead of algebraic ones). This serves a transcendental equation which can be solved numerically. The figure shows a comparison of the Kibble–Zurek scaling with algebraic and exponential divergences. The data illustrate, that the Kibble–Zurek mechanism also works for transitions of the Kosterlitz–Thoules universality class.