Physics:Kovasznay flow
Kovasznay flow corresponds to an exact solution of the Navier–Stokes equations and are interpreted to describe the flow behind a two-dimensional grid. The flow is named after Leslie Stephen George Kovasznay, who discovered this solution in 1948.[1] The solution is often used to validate numerical codes solving two-dimensional Navier-Stokes equations.
Flow description
Let [math]\displaystyle{ U }[/math] be the free stream velocity and let [math]\displaystyle{ L }[/math] be the spacing between a two-dimensional grid. The velocity field [math]\displaystyle{ (u,v,0) }[/math] of the Kovaszany flow, expressed in the Cartesian coordinate system is given by[2]
- [math]\displaystyle{ \frac{u}{U} = 1- e^{\lambda x/L}\cos\left(\frac{2\pi y}{L}\right), \quad \frac{v}{U} = -\frac{\lambda}{2\pi} \sin\left(\frac{2\pi y}{L}\right) }[/math]
where [math]\displaystyle{ \lambda }[/math] is the root of the equation [math]\displaystyle{ \lambda^2-Re\, \lambda -4\pi^2=0 }[/math] in which [math]\displaystyle{ Re=UL/\nu }[/math] represents the Reynolds number of the flow. The root that describes the flow behind the two-dimensional grid is found to be
- [math]\displaystyle{ \lambda = \frac{1}{2}(Re-\sqrt{Re^2+16\pi^2}). }[/math]
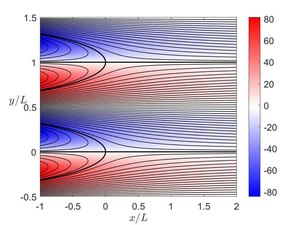
The corresponding vorticity field [math]\displaystyle{ (0,0,\omega) }[/math] and the stream function [math]\displaystyle{ \psi }[/math] are given by
- [math]\displaystyle{ \frac{\omega}{U/L}=Re\lambda e^{\lambda x/L}\sin\left(\frac{2\pi y}{L}\right), \quad \frac{\psi}{LU} = \frac{y}{L}- \frac{1}{2\pi}e^{\lambda x/L}\cos\left(\frac{2\pi y}{L}\right). }[/math]
Similar exact solutions, extending Kovasznay's, has been noted by Lin and Tobak[3] and C. Y. Wang.[4][5]
References
- ↑ Kovasznay, L. I. G. (1948, January). Laminar flow behind a two-dimensional grid. In Mathematical Proceedings of the Cambridge Philosophical Society (Vol. 44, No. 1, pp. 58-62). Cambridge University Press.
- ↑ Drazin, P. G., & Riley, N. (2006). The Navier-Stokes equations: a classification of flows and exact solutions (No. 334). Cambridge University Press. page 17
- ↑ Lin, S. P., & Tobak, M. (1986). Reversed flow above a plate with suction. AIAA journal, 24(2), 334-335.
- ↑ Wang, C. Y. (1966). On a class of exact solutions of the Navier-Stokes equations. Journal of Applied Mechanics, 33(3), 696-698.
- ↑ Wang, C. Y. (1991). Exact solutions of the steady-state Navier-Stokes equations. Annual Review of Fluid Mechanics, 23(1), 159-177.
 |