Physics:Landau–Squire jet

In fluid dynamics, Landau–Squire jet or Submerged Landau jet describes a round submerged jet issued from a point source of momentum into an infinite fluid medium of the same kind. This is an exact solution to the incompressible form of the Navier-Stokes equations, which was first discovered by Lev Landau in 1944 and later by Herbert Squire in 1951. The self-similar equation was in fact first derived by N. A. Slezkin in 1934, but never applied to the jet. Following Landau's work, V. I. Yatseyev obtained the general solution of the equation in 1950.

Mathematical description

Landau-Squire jet streamlines for c=0.01

Landau-Squire jet streamlines for c=0.1

Landau-Squire jet streamlines for c=1

The problem is described in spherical coordinates [math]\displaystyle{ (r,\theta,\phi) }[/math] with velocity components [math]\displaystyle{ (u,v,0) }[/math]. The flow is axisymmetric, i.e., independent of [math]\displaystyle{ \phi }[/math]. Then the continuity equation and the incompressible Navier–Stokes equations reduce to

[math]\displaystyle{ \begin{align} & \frac{1}{r^2} \frac{\partial }{\partial r}(r^2u) + \frac{1}{r\sin\theta}\frac{\partial }{\partial \theta}(v\sin\theta) = 0 \\[8pt] & u\frac{\partial u}{\partial r} + \frac{v}{r} \frac{\partial u}{\partial \theta} - \frac{v^2}{r}= - \frac{1}{\rho} \frac{\partial p}{\partial r} + \nu \left(\nabla^2 u - \frac{2u}{r^2} - \frac{2}{r^2} \frac{\partial v}{\partial \theta} - \frac{2v\cot\theta}{r^2} \right) \\[8pt] & u\frac{\partial v}{\partial r} + \frac{v}{r}\frac{\partial v}{\partial \theta} + \frac{uv}{r} = -\frac{1}{\rho r} \frac{\partial p}{\partial \theta} + \nu \left(\nabla^2 v + \frac{2}{r^2}\frac{\partial u}{\partial \theta} - \frac{v}{r^2\sin^2\theta}\right) \end{align} }[/math]

where

[math]\displaystyle{ \nabla^2 = \frac{1}{r^2} \frac{\partial }{\partial r}\left(r^2 \frac{\partial }{\partial r}\right) + \frac{1}{r^2\sin\theta}\frac{\partial }{\partial \theta}\left(\sin\theta\frac{\partial }{\partial \theta}\right). }[/math]

A self-similar description is available for the solution in the following form,

[math]\displaystyle{ u = \frac{\nu}{r\sin\theta} f'(\theta),\quad v = -\frac{\nu}{r\sin\theta} f(\theta). }[/math]

Substituting the above self-similar form into the governing equations and using the boundary conditions [math]\displaystyle{ u=v=p-p_\infty=0 }[/math] at infinity, one finds the form for pressure as

[math]\displaystyle{ \frac{p-p_\infty}{\rho} = -\frac{v^2}{2} + \frac{\nu u}{r} + \frac{c_1}{r^2} }[/math]

where [math]\displaystyle{ c_1 }[/math] is a constant. Using this pressure, we find again from the momentum equation,

[math]\displaystyle{ -\frac{u^2}{r} + \frac{v}{r} \frac{\partial u}{\partial \theta} = \frac{\nu}{r^2} \left[2u + \frac{1}{\sin\theta} \frac{\partial }{\partial \theta} \left(\sin\theta\frac{\partial u}{\partial \theta}\right)\right] + \frac{2c_1}{r^3}. }[/math]

Replacing [math]\displaystyle{ \theta }[/math] by [math]\displaystyle{ \mu=\cos\theta }[/math] as independent variable, the velocities become

[math]\displaystyle{ u = -\frac{\nu}{r} f'(\mu),\quad v = -\frac{\nu}{r} \frac{f(\mu)}{\sqrt{1-\mu^2}} }[/math]

(for brevity, the same symbol is used for [math]\displaystyle{ f(\theta) }[/math] and [math]\displaystyle{ f(\mu) }[/math] even though they are functionally the same, but takes different numerical values) and the equation becomes

[math]\displaystyle{ f'^2 + ff'' = 2f' + [(1-\mu^2)f'']' - 2c_1. }[/math]

After two integrations, the equation reduces to

[math]\displaystyle{ f^2 = 4\mu f + 2(1-\mu^2) f' - 2(c_1\mu^2 + c_2 \mu + c_3), }[/math]

where [math]\displaystyle{ c_2 }[/math] and [math]\displaystyle{ c_3 }[/math] are constants of integration. The above equation is a Riccati equation. After some calculation, the general solution can be shown to be

[math]\displaystyle{ f = \alpha(1+\mu) + \beta(1-\mu) + \frac{2(1-\mu^2)(1+\mu)^\beta}{(1-\mu)^\alpha}\left[c- \int_1^\mu \frac{(1+\mu)^\beta}{(1-\mu)^\alpha}\right]^{-1}, }[/math]

where [math]\displaystyle{ \alpha,\ \beta,\ c }[/math] are constants. The physically relevant solution to the jet corresponds to the case [math]\displaystyle{ \alpha=\beta=0 }[/math] (Equivalently, we say that [math]\displaystyle{ c_1=c_2=c_3=0 }[/math], so that the solution is free from singularities on the axis of symmetry, except at the origin). Therefore,

[math]\displaystyle{ f = \frac{2(1-\mu^2)}{c+1-\mu} = \frac{2\sin^2\theta}{c+1-\cos\theta}. }[/math]

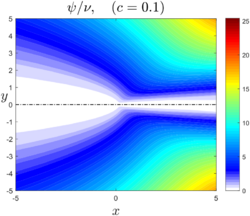
The function [math]\displaystyle{ f }[/math] is related to the stream function as [math]\displaystyle{ \psi = \nu r f }[/math], thus contours of [math]\displaystyle{ f }[/math] for different values of [math]\displaystyle{ c }[/math] provides the streamlines. The constant [math]\displaystyle{ c }[/math] describes the force at the origin acting in the direction of the jet (this force is equal to the rate of momentum transfer across any sphere around the origin plus the force in the jet direction exerted by the sphere due to pressure and viscous forces), the exact relation between the force and the constant is given by

[math]\displaystyle{ \frac{F}{2\pi\rho \nu^2} = \frac{32(c+1)}{3c(c+2)} + 8(c+1) - 4(c+1)^2\ln \frac{c+2}{c} . }[/math]

The solution describes a jet of fluid moving away from the origin rapidly and entraining the slowly moving fluid outside of the jet. The edge of the jet can be defined as the location where the streamlines are at minimum distance from the axis, i.e., the edge is given by

[math]\displaystyle{ \theta_o = \cos^{-1} \left(\frac{1}{1+c}\right). }[/math]

Therefore, the force can be expressed alternatively using this semi-angle of the conical-boundary of the jet,

[math]\displaystyle{ \frac{F}{2\pi \rho \nu^2} = \frac{32}{3}\frac{\cos\theta_o}{\sin^2\theta_o} +\frac{4}{\cos\theta_o} \ln \frac{1-\cos\theta_o}{1+\cos\theta_o} + \frac{8}{\cos\theta_o}. }[/math]

Limiting behaviors

When the force becomes large, the semi-angle of the jet becomes small, in which case,

[math]\displaystyle{ \frac{F}{2\pi \rho \nu^2} \sim \frac{32}{3\theta_o^2} \ll 1 }[/math]

and the solution inside and outside of the jet become

[math]\displaystyle{ \begin{align} f(\theta)&\sim \frac{4\theta^2}{\theta^2+\theta_o^2},\quad \theta\lt \theta_o,\\ f(\theta)&\sim 2(1+\cos\theta),\quad \theta\gt \theta_o. \end{align} }[/math]

The jet in this limiting case is called the Schlichting jet. On the other extreme, when the force is small,

[math]\displaystyle{ \frac{F}{2\pi \rho \nu^2} \sim \frac{8}{c}\gg 1 }[/math]

the semi-angle approaches 90 degree (no inside and outside region, the whole domain is considered as single region), the solution itself goes to

[math]\displaystyle{ f(\theta)\sim\frac{2}{c}\sin^2\theta. }[/math]

See also

• Schlichting jet
• Schneider flow