Physics:Magnetic tension

Short description: Restoring force on bent magnetic field lines

The magnetic tension force, depicted by the red arrow, acts to straighten the bent magnetic field lines in black.

In physics, magnetic tension is a restoring force with units of force density that acts to straighten bent magnetic field lines. In SI units, the force density [math]\displaystyle{ \mathbf{f}_T }[/math] exerted perpendicular to a magnetic field [math]\displaystyle{ \mathbf{B} }[/math] can be expressed as

[math]\displaystyle{ \mathbf{f}_T = \frac{\left(\mathbf{B} \cdot \nabla\right)\mathbf{B}}{\mu_0} }[/math]

where [math]\displaystyle{ \mu_0 }[/math] is the vacuum permeability.

Magnetic tension forces also rely on vector current densities and their interaction with the magnetic field. Plotting magnetic tension along adjacent field lines can give a picture as to their divergence and convergence with respect to each other as well as current densities.

Magnetic tension is analogous to the restoring force of rubber bands.

Mathematical statement

In ideal magnetohydrodynamics (MHD) the magnetic tension force in an electrically conducting fluid with a bulk plasma velocity field [math]\displaystyle{ \mathbf{v} }[/math], current density [math]\displaystyle{ \mathbf{J} }[/math], mass density [math]\displaystyle{ \rho }[/math], magnetic field [math]\displaystyle{ \mathbf{B} }[/math], and plasma pressure [math]\displaystyle{ p }[/math] can be derived from the Cauchy momentum equation:

[math]\displaystyle{ \rho\left(\frac{\partial}{\partial t} + \mathbf{v} \cdot \nabla\right)\mathbf{v} = \mathbf{J}\times\mathbf{B} - \nabla p, }[/math]

where the first term on the right hand side represents the Lorentz force and the second term represents pressure gradient forces. The Lorentz force can be expanded using Ampère's law, [math]\displaystyle{ \mu_0\mathbf{J} = \nabla \times \mathbf{B} }[/math], and the vector identity

[math]\displaystyle{ \tfrac12\nabla(\mathbf{B}\cdot \mathbf{B})=(\mathbf{B}\cdot\nabla)\mathbf{B}+\mathbf{B}\times(\nabla\times \mathbf{B}) }[/math]

to give

[math]\displaystyle{ \mathbf{J} \times \mathbf{B} = {(\mathbf{B} \cdot \nabla)\mathbf{B} \over \mu_0} - \nabla\left(\frac{B^2}{2\mu_0}\right), }[/math]

where the first term on the right hand side is the magnetic tension and the second term is the magnetic pressure force.

The force due to changes in the magnitude of [math]\displaystyle{ \mathbf{B} }[/math] and its direction can be separated by writing [math]\displaystyle{ \mathbf{B} = B\mathbf{b} }[/math] with [math]\displaystyle{ B = |\mathbf{B}| }[/math] and [math]\displaystyle{ \mathbf{b} }[/math] a unit vector:

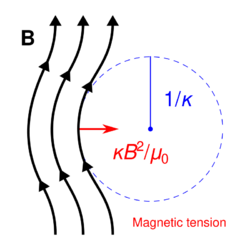
[math]\displaystyle{ {(\mathbf{B} \cdot \nabla)\mathbf{B} \over \mu_0} = \frac{B^2}{\mu_0}(\mathbf{b} \cdot \nabla) \mathbf{b} = \frac{B^2}{\mu_0}\boldsymbol\kappa }[/math]

where the spatial constancy of the magnitude has been assumed [math]\displaystyle{ \nabla B=0 }[/math] and

[math]\displaystyle{ \boldsymbol\kappa = (\mathbf{b} \cdot \nabla) \mathbf{b} }[/math]

has magnitude equal to the curvature, or the reciprocal of the radius of curvature, and is directed from a point on a magnetic field line to the center of curvature. Therefore, as the curvature of the magnetic field line increases, so too does the magnetic tension force resisting this curvature.

Magnetic tension and pressure are both implicitly included in the Maxwell stress tensor. Terms representing these two forces are present along the main diagonal where they act on differential area elements normal to the corresponding axis.

Plasma physics

Magnetic tension is particularly important in plasma physics and MHD, where it controls dynamics of some systems and the shape of magnetic structures. For example, in a homogeneous magnetic field and an absence of gravity, magnetic tension is the sole driver of linear Alfvén waves.

See also

• Magnetic pinch
• Magnetosonic wave