Physics:Magneto-optic Kerr effect

In physics the magneto-optic Kerr effect (MOKE) or the surface magneto-optic Kerr effect (SMOKE) is one of the magneto-optic effects. It describes the changes to light reflected from a magnetized surface. It is used in materials science research in devices such as the Kerr microscope, to investigate the magnetization structure of materials.

Several grains of NdFeB with magnetic domains made visible via contrast with a Kerr-microscope.

Definition

The magneto-optic Kerr effect manifests when light is reflected from a magnetized surface and may change both polarization and reflected intensity. The magneto-optic Kerr effect is similar to the Faraday effect, which describes changes to light transmission through a magnetic material. In contrast, the magneto-optic Kerr effect describes changes to light reflected from a magnetic surface. Both effects result from the off-diagonal components of the dielectric tensor [math]\displaystyle{ \varepsilon }[/math]. These off-diagonal components give the magneto-optic material an anisotropic permittivity, meaning that its permittivity is different in different directions. The permittivity affects the speed of light in a material:

[math]\displaystyle{ v_p = \frac{1}{\sqrt{\varepsilon \mu}} }[/math]

where [math]\displaystyle{ v_p }[/math] is the velocity of light through the material, [math]\displaystyle{ \varepsilon }[/math] is the material permittivity, and [math]\displaystyle{ \mu }[/math] is the magnetic permeability; and thus the speed of light varies depending on its orientation. This causes fluctuations in the phase of polarized incident light.

This effect is often quantified in terms of its Kerr angle and its Kerr ellipticity. The Kerr angle [math]\displaystyle{ \theta_k }[/math] is the angle that linearly polarized light will be rotated after hitting the sample. The Kerr ellipticity [math]\displaystyle{ \epsilon_k }[/math] or [math]\displaystyle{ \eta_k }[/math](not to be confused with ellipticity from mathematics) is the ratio of the semimajor and semiminor axes of the elliptically polarized light, generated from reflection of linearly polarized light.

Geometries

MOKE can be further categorized by the direction of the magnetization vector with respect to the reflecting surface and the plane of incidence.

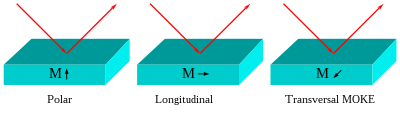
Polar MOKE

When the magnetization vector is perpendicular to the reflection surface and parallel to the plane of incidence, the effect is called the polar Kerr effect. To simplify the analysis, and because the other two configurations have vanishing Kerr rotation at normal incidence, near normal incidence is usually employed when doing experiments in the polar geometry.

Longitudinal MOKE

In the longitudinal effect, the magnetization vector is parallel to both the reflection surface and the plane of incidence. The longitudinal setup involves light reflected at an angle from the reflection surface and not normal to it, as is used for polar MOKE. In the same manner, linearly polarized light incident on the surface becomes elliptically polarized, with the change in polarization directly proportional to the component of magnetization that is parallel to the reflection surface and parallel to the plane of incidence. This elliptically polarized light to first-order has two perpendicular [math]\displaystyle{ E }[/math] vectors, namely the standard Fresnel amplitude coefficient of reflection [math]\displaystyle{ r }[/math] and the Kerr coefficient [math]\displaystyle{ k }[/math]. The Kerr coefficient is typically much smaller than the coefficient of reflection.

Transversal MOKE

When the magnetization is perpendicular to the plane of incidence and parallel to the surface it is said to be in the transverse configuration. In this case, the incident light is also not normal to the reflection surface but instead of measuring the polarity of the light after reflection, the reflectivity [math]\displaystyle{ r }[/math] is measured. This change in reflectivity is proportional to the component of magnetization that is perpendicular to the plane of incidence and parallel to the surface, as above. If the magnetization component points to the right of the incident plane, as viewed from the source, then the Kerr vector adds to the Fresnel amplitude vector and the intensity of the reflected light is [math]\displaystyle{ |r+k|^2 }[/math]. On the other hand, if the component of magnetization component points to the left of the incident plane as viewed from the source, the Kerr vector subtracts from the Fresnel amplitude and the reflected intensity is given by [math]\displaystyle{ |r-k|^2 }[/math].

Quadratic MOKE

In addition to the polar, longitudinal and transverse Kerr effect which depend linearly on the respective magnetization components, there are also higher order quadratic effects, for which the Kerr angle depends on product terms involving the polar, longitudinal and transverse magnetization components. Those effects are referred to as Voigt effect or quadratic Kerr effect. Quadratic magneto-optic Kerr effect (QMOKE) is found strong in Heusler alloys such as Co₂FeSi and Co₂MnGe

Applications

Optical experiment for observing the Magneto-optic Kerr effect

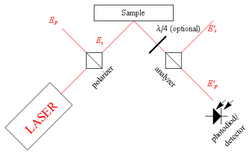
Microscopy

A Kerr microscope relies on the MOKE in order to image differences in the magnetization on a surface of magnetic material. In a Kerr microscope, the illuminating light is first passed through a polarizer filter, then reflects from the sample and passes through an analyzer polarizing filter, before going through a regular optical microscope. Because the different MOKE geometries require different polarized light, the polarizer should have the option to change the polarization of the incident light (circular, linear, and elliptical). When the polarized light is reflected off the sample material, a change in any combination of the following may occur: Kerr rotation, Kerr ellipticity, or polarized amplitude. The changes in polarization are converted by the analyzer into changes in light intensity, which are visible. A computer system is often used to create an image of the magnetic field on the surface from these changes in polarization.

Magnetic Media

Magneto Optical (MO) Drives were introduced in 1985. MO discs were written using a laser and an electromagnet. The laser would heat the platter above its Curie temperature at which point the electromagnet would orient that bit as a 1 or 0. To read, the laser is operated at a lower intensity, and emits polarized light. Reflected light is analyzed showing a noticeable difference between a 0 or 1.

Discovery

The magneto-optic Kerr effect was discovered in 1877 by John Kerr.

See also

• Faraday effect
• Fresnel equations
• John Kerr
• Thin-film optics
• Voigt Effect
• Zeeman Effect

Further reading

• Zvezdin A.K.; Kotov V.A. (1997). Modern magnetooptics and magnetooptical materials. Institute of Physics Publishing. p. 404. ISBN 978-0-7503-0362-0. 
• Etienne Du Trémolet de Lacheisserie, ed (2005). Magnetism Fundamentals I. Springer Science & Business Media. p. 507. ISBN 978-0-387-22967-6. https://www.springer.com/gp/book/9780387229676. 

External links

• Kerr Calculation Applet – Java applet, computes the Kerr angle of multilayered thin films
• yeh-moke – Free software computes the Magneto-optic Kerr effect of multilayered thin films
• MOKE Microscope – Magneto-Optical Kerr Effect Microscope [PDF: 3.2MB]
• MOKE tutorial – A step by step tutorial on the longitudinal, polar and transverse Magneto-Optical Kerr Effect.
• Broadband magneto-optical Kerr spectroscopy