Physics:Malus-Dupin theorem
The Malus-Dupin theorem is a theorem in geometrical optics discovered by Étienne-Louis Malus in 1808[1] and clarified by Charles Dupin in 1822.[2] Hamilton proved it as a simple application of his Hamiltonian optics method[3].[4]
Consider a pencil of light rays in a homogenous medium that is perpendicular to some surface. Pass the pencil of rays through an arbitrary amount of reflections and refractions, then let it emerge in some other homogenous medium. The theorem states that the resulting pencil of light rays is still perpendicular to some other surface.
Implications
This section needs additional citations for verification. (July 2023) (Learn how and when to remove this template message) |
Some ray pencils are not perpendicular to any surface. This is related to contact geometry.
For example, consider the standard contact structure on R3, which can be understood as a field of infinitesimal planes. Now, perpendicular to every infinitesimal plane, draw a light ray. This gives us a "planar twisted" pencil of light rays. There is no surface perpendicular to the pencil, because there is no surface that can be tangent to every infinitesimal plane.
Suppose there is, then draw an infinitesimal square in the x-y plane, and follow the path along the surface. The path would not return to the same z-coordinate after one circuit. Contradiction.
Similarly, one can nest a sequence of circular pencils, each making up a hyperboloid of one-sheet. The resulting "twisted cylinder" pencil would not be perpendicular to any surface.
Malus-Dupin theorem implies that no amount of reflection and refraction could convert such a pencil of rays into a pencil of parallel rays, or a pencil of rays converging on one point, or any pencil of rays that are perpendicular to a surface.
Construction and proof
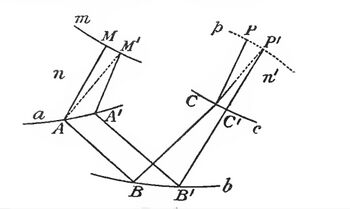
Given a pencil of rays, suppose that the pencil of rays is perpendicular to a surface m at the beginning.[5]
Pass the pencil of rays through an arbitrary system of reflecting and refracting material. For illustration, consider two rays refracted at points A and A'; reflected at points B and B'; and refracted points C and C'.
Now take two rays from the pencil: [MABCP] and [M'A'B'C'P']. Let the two rays be perpendicular to m at points M and M' respectively.
Choose point P' so that [MABCP] and [M'A'B'C'P'] have the same optical path; then the set of all P, P' with equal optical path forms a curved surface p.
Theorem — The surface p is orthogonal to the pencil of rays.
Take two rays from the pencil: [MABCP] and [M'A'B'C'P'], that are infinitesimally close. Draw line segments M'A and P'C.
Since M'A is perpendicular to surface m, we have [M'A] ~ [MA], thus
[MABCP'] ~ [M'ABCP']
[M'ABCP']~[M'A'B'C'P']
By construction, [M'A'B'C'P']=[MABCP],
Together, we have
[MABCP']~[MABCP];
which implies [CP'] ~ [CP], thus the surface p is perpendicular to CP at P.
References
- ↑ É. L. Malus, Journal de l’École Polytechnique 7, pp. 1–44 and 84–129.
- ↑ C. Dupin, Applications de la géométrie, Mémoire présenté à l’Académie des Sciences en 1816, publié à Paris en 1822.
- ↑ W. R. Hamilton, Theory of systems of rays, Part First and Part Second. Part first: Trans. Royal Irish Academy, 15, pp. 69–174. Part Second: manuscript. In Sir William Rowan Hamilton mathematical Works, vol. I, chapter I, Cambridge University Press, London, 1931
- ↑ Marle, Charles-Michel (2016). "The works of William Rowan Hamilton in geometrical optics and the Malus-Dupin theorem". Banach Center Publications 110: 177–191. doi:10.4064/bc110-0-12. ISSN 0137-6934.
- ↑ Moritz von Rohr ed. Geometrical Investigation of the Formation of Images in Optical Instruments M.M.STATIONARY,LONDON 1920, page 21
 |