Physics:Mass-spring-damper model

Short description: Concept in physics

Classic model used for deriving the equations of a mass spring damper model

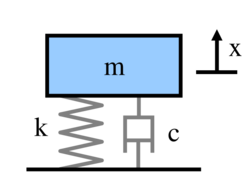
The mass-spring-damper model consists of discrete mass nodes distributed throughout an object and interconnected via a network of springs and dampers.

This form of model is also well-suited for modelling objects with complex material behavior such as those with nonlinearity or viscoelasticity.

As well as engineering simulation, these systems have applications in computer graphics and computer animation.

Derivation (Single Mass)

Deriving the equations of motion for this model is usually done by summing the forces on the mass (including any applied external forces $F_{\text{external}})$:

$\mathrm{\Sigma }F=-kx-c\dot{x}+F_{\text{external}}=m\ddot{x}$

By rearranging this equation, we can derive the standard form:

$\ddot{x}+2\zeta {\omega }_n\dot{x}+{\omega }_n^{2}x=u$ where ${\omega }_n=\sqrt{\frac{k}{m}};\zeta =\frac{c}{2m{\omega }_n};u=\frac{F_{\text{external}}}{m}$

${\omega }_n$ is the undamped natural frequency and $\zeta$ is the damping ratio. The homogeneous equation for the mass spring system is:

$\ddot{x}+2\zeta {\omega }_n\dot{x}+{\omega }_n^{2}x=0$

This has the solution:

$x=A{e}^{-{\omega }_{n}t(\zeta +\sqrt{{\zeta }^2-1})}+B{e}^{-{\omega }_{n}t(\zeta -\sqrt{{\zeta }^2-1})}$

If $\zeta <1$ then ${\zeta }^2-1$ is negative, meaning the square root will be imaginary and therefore the solution will have an oscillatory component.

See also

• Numerical methods
• Soft body dynamics#Spring/mass models
• Finite element analysis