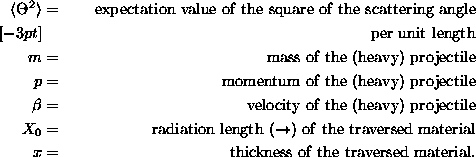Physics:Multiple scattering

Effect of Coulomb scattering acting on a particle and summing up in the way of many relatively small random changes of the direction of flight. For a thin layer of traversed material the variance of the projected scattering angle of a particle with unit charge can be approximated by

where

The underlying assumption of a Gaussian distribution makes this approximation a crude one; in particular, large angles are underestimated by the Gaussian form. For more details see Rossi65, Scott63, Fernow86, Barnett96.

In the general case, the scattering effect, considered as white noise, is described by

with s = path length, = influence of the scattering angle at s on the impact point C in detector k, and = white noise.

For a straight track in a homogeneous medium and with detectors perpendicular to the track , y(0)=0, , it follows that

and with (writing for )  :

and similarly

or written as a matrix

Up to quadratic properties this is equivalent to the Gaussian probability density function

The effects of multiple scattering on track reconstruction were first described by Gluckstern Gluckstern63. In track fitting a matrix formalism for multiple scattering can be used. To the (usually diagonal) covariance matrix describing the detector resolution a non-diagonal term taking into account multiple scattering must be added:

where File:Hepb img434.gif is a random variable describing the change of the ith measurement due to multiple scattering for particles travelling parallel to the x-axis and detectors normal to this axis, and E stands for expectation value.

For discrete scatterers (obstacles) and particles moving parallel to the x-axis and detectors normal to this axis, this covariance matrix is given by

The sum is over all obstacles with .

A detailed discussion of this matrix formalism is given in Eichinger81.