Physics:Néel effect

In superparamagnetism (a form of magnetism), the Néel effect appears when a superparamagnetic material in a conducting coil is subject to varying frequencies of magnetic fields. The non-linearity of the superparamagnetic material acts as a frequency mixer, with voltage measured at the coil terminals. It consists of several frequency components, at the initial frequency and at the frequencies of certain linear combinations. The frequency shift of the field to be measured allows for detection of a direct current field with a standard coil.

Magnetizing superparamagnetic material

History

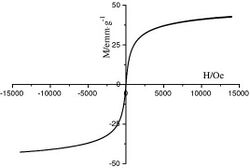
In 1949 French physicist Louis Néel (1904-2000) discovered that when they are finely divided, ferromagnetic nanoparticles lose their hysteresis below a certain size; this phenomenon is known as superparamagnetism. The magnetization of these materials is subject to the applied field, which is highly non-linear.

This curve is well described by the Langevin function, but for weak fields it can be simply written as:

[math]\displaystyle{ M(H) = \chi_0H + N_eH^3 + \varepsilon(H^3) }[/math],

where [math]\displaystyle{ \chi_0 }[/math] is the susceptibility at zero field and [math]\displaystyle{ N_e }[/math] is known as the Néel coefficient. The Néel coefficient reflects the non-linearity of superparamagnetic materials in low fields.

Theory

Illustration of the Néel effect

If a coil of [math]\displaystyle{ N }[/math] turns with a surface [math]\displaystyle{ S }[/math] through which passes a current of excitation [math]\displaystyle{ I_\text{exc} }[/math] is immersed in a magnetic field [math]\displaystyle{ H_{ext} }[/math] collinear with the axis of the coil, a superparamagnetic material is deposited inside the coil.

The electromotive force to the terminals of a winding of the coil, [math]\displaystyle{ e }[/math], is given by the formula:

[math]\displaystyle{ e = -d\phi /dt = - SdB/dt }[/math]

where [math]\displaystyle{ B }[/math] is the magnetic induction given by the equation:

[math]\displaystyle{ B = \mu_0 \mu_r (H + M) }[/math]

In the absence of magnetic material,

[math]\displaystyle{ M = 0 }[/math]

and

[math]\displaystyle{ B = \mu_0 \mu_r (H_{ext} + H_\text{exc}) }[/math].

Differentiating this expression, the frequency of the voltage is the same as the excitation current [math]\displaystyle{ i_\text{exc} }[/math] or the magnetic field [math]\displaystyle{ H_{ext} }[/math].

In the presence of superparamagnetic material, neglecting the higher terms of the Taylor expansion, we obtain for B:

[math]\displaystyle{ B = \mu_0\mu_r((1 + \chi_0)(H_{ext} + H_\text{exc}) + N_e (H_{ext} + H_\text{exc})^3) }[/math]

A new derivation of the first term of the equation [math]\displaystyle{ \mu_0 \mu_r (1 + \chi_0) (H_{ext} + H_\text{exc}) }[/math] provides frequency voltage components of the stream of excitement [math]\displaystyle{ i_\text{exc} }[/math] or the magnetic field [math]\displaystyle{ H_{ext} }[/math].

The development of the second term [math]\displaystyle{ (H_{ext} + H_\text{exc})^3 = H_{ext}^3 + 3H_{ext}^2H_\text{exc} + 3H_{ext}H_\text{exc}^2 + H_\text{exc}^3 }[/math] multiplies the frequency components in which intermodular frequencies start components and generate their linear combinations. The non-linearity of the superparamagnetic material acts as a frequency mixer.

Calling [math]\displaystyle{ H(l) }[/math] the total magnetic field within the coil at the abscissa, integrating the above induction coil along the abscissa between 0 and [math]\displaystyle{ L_p }[/math] and differentiating with respect to [math]\displaystyle{ t }[/math] obtains:

[math]\displaystyle{ u(t) = L \frac{dI(t)}{dt} + F_{Rog} \frac{d}{dt} \left[\int_0^{H} Lp(l) dl \right] + F_\text{Neel} \left[\int_0^H Lp(l) dl \right] I(t) \frac{dI(t)}{dt} }[/math]

with [math]\displaystyle{ I_\text{exc}(t) = I_\text{exc}\cos(w_\text{exc}t) }[/math]

Spectral representation of the appearance of EMF due to the Néel effect around a high-frequency carrier

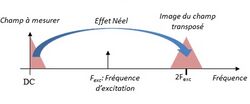
The conventional terms of self-inductance and Rogowski effect are found in both the original frequencies. The third term is due to the Néel effect; it reports the intermodulation between the excitation current and the external field.

When the excitation current is sinusoidal, the effect is Néel characterized by the appearance of a second harmonic carrying the information flow field:

[math]\displaystyle{ u(t) = LI_\text{exc}w_\text{exc}\cos(w_\text{exc}t) + F_{Rog}\frac{d}{dt}\left[\int_0^{Lp}H_{ext}(l)dl\right] + F_\text{Neel}\left[\int_0^{Lp}H_{ext}(l)dl\right]\frac{I_\text{exc}^2}{2}w_\text{exc}\sin(2w_\text{exc}t) }[/math]

Applications

Design of Néel-effect current sensor

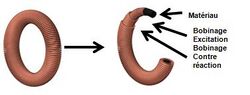
An important application of the Néel effect is as a current sensor, measuring the magnetic field radiated by a conductor with a current; this is the principle of Néel effect current sensors. The Néel effect allows the accurate measurement of currents with very low-frequency-type sensors in a current transformer without contact.

The transducer of a Néel-effect current sensor consists of a coil with a core of superparamagnetic nanoparticles. The coil is traversed by a current excitation:

[math]\displaystyle{ i_\text{exc}(t) }[/math].

In the presence of an external magnetic field to be measured:

[math]\displaystyle{ H_{ext}(t) }[/math]

the transducer transposes (with the Néel effect) the information to be measured, H (f) around a carrier frequency, the harmonic of order 2 excitation current 2:

[math]\displaystyle{ f_\text{exc} }[/math]

which is simpler. The electromotive force generated by the coil is proportional to the magnetic field to measure:

[math]\displaystyle{ H_{ext}(t) }[/math]

and to the square of the excitation current:

[math]\displaystyle{ fem(t) = F_\text{Neel} i_\text{exc}^2(t) H(t) }[/math]

To improve the measurement's performance (such as linearity and sensitivity to temperature and vibration), the sensor includes a second permanent winding-reaction against it to cancel the second harmonic. The relationship of the current reaction against the primary current is proportional to the number of turns against reaction:

[math]\displaystyle{ I_{cr} = I_p / N_{cr} }[/math].

See also

• Superparamagnetism
• Louis Néel