Physics:PP/2/Particle Decays

<< Back

20% complete

Section [[Physics:PP/2/Relativistic_Kinematics|Relativistic Kinematics introduced a basic definitions that can be used to consider particle decays. Here will will discuss in more detail most common situations.

Cascade decays

A cascade decays is another common situation. For example, top quarks decay to b-quark and W bosons, where W can decay to a [math]\displaystyle{ q\bar{q} }[/math] pair.

Let us make a simple calculator that estimates the average angle between W boson and q for highly boosted top quarks with momenta 1 TeV (1 TeV=1000 GeV). We will use a Monte Carlo techniques that decay top and W, randomize angles, and boost decay products to the top-quark rest frame. We will use the  LParticle class.

from jhplot  import *
from java.util import Random
from hephysics.particle import *
from math import *

Top=LParticle("Top",175.0)
W,b = LParticle("W",80.38), LParticle("b",4.18)
q1,q2 = LParticle("q1",0.004), LParticle("q2",0.004)
P=1000 # top quark has Pz=1 TeV momentum
Top.setPxPyPzE(0,0,P,sqrt(P*P+175**2))
print Top.toString()
r = Random()
h1 = H1D("maxAngle",40, 0,100)
for i in xrange(50000):
     if (i%2000==0): print "event=",i
     Top.twoBodyDecay(W, b,1);
     theta = acos( 2.0*r.nextDouble() - 1.0 )
     phi   = 2*pi*r.nextDouble()
     Top.setThetaPhiP(theta,phi,P)
     W.boost( Top )
     b.boost( Top )
     W.twoBodyDecay(q1,q2,1)
     q1.boost( W )
     q2.boost( W )
     h1.fill(degrees(W.angle(q1)))
     h1.fill(degrees(W.angle(q2)))

c1 = HPlot()
c1.visible(1)
c1.setMarginLeft(100)
c1.setRange(0,100,0,25000)
c1.setNameX("θ_{Max} [deg]")
c1.setNameY("Events")
c1.draw(h1)
c1.drawStatBox(h1)
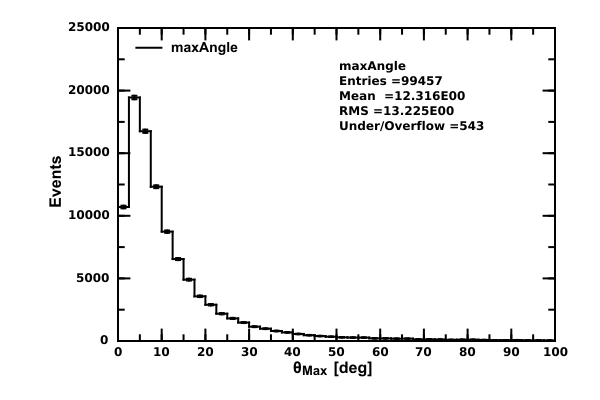
c1.export("ppbook_c2_p1.svg")

The output is

You can see the the average angle between W and quarks is about 12 degrees. One can change P=1000 to a lower value and you will see that the plotted angle will significantly increase. Such simple calculations are very useful for designing experiments where the knowledge of angles between particle decay products are useful in determining detector resolutions.