Physics:Painlevé conjecture

From HandWiki
Short description: Physical theorem
Jeff Xia's 5-body configuration consists of five point masses, with two pairs in eccentric elliptic orbits around each other and one mass oscillating forwards and backwards along the line of symmetry. Xia proved that for certain initial conditions the final mass will be accelerated to infinite velocity in finite time. This proves the Painlevé conjecture for five bodies and upwards.

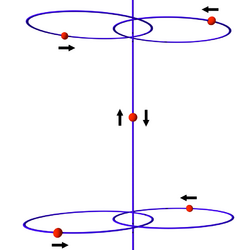
In physics, the Painlevé conjecture is a theorem about singularities among the solutions to the n-body problem: there are noncollision singularities for n ≥ 4.[1][2]

The theorem was proven for n ≥ 5 in 1988 by Jeff Xia[3][4] and for n=4 in 2014 by Jinxin Xue.[5][6]


Background and statement

Solutions [math]\displaystyle{ (\mathbf{q},\mathbf{p}) }[/math] of the n-body problem [math]\displaystyle{ \dot{\mathbf{q}} = M^{-1}\mathbf{p},\; \dot{\mathbf{p}} = \nabla U(\mathbf{q}) }[/math] (where M are the masses and U denotes the gravitational potential) are said to have a singularity if there is a sequence of times [math]\displaystyle{ t_n }[/math] converging to a finite [math]\displaystyle{ t^* }[/math] where [math]\displaystyle{ \nabla U\left(\mathbf{q}\left(t_n\right)\right) \rightarrow \infty }[/math]. That is, the forces and accelerations become infinite at some finite point in time.

A collision singularity occurs if [math]\displaystyle{ \mathbf{q}(t) }[/math] tends to a definite limit when [math]\displaystyle{ t \rightarrow t^*, t\lt t^* }[/math]. If the limit does not exist the singularity is called a pseudocollision or noncollision singularity.

Paul Painlevé showed that for n = 3 any solution with a finite time singularity experiences a collision singularity. However, he failed at extending this result beyond 3 bodies. His 1895 Stockholm lectures end with the conjecture that

For n ≥ 4 the n-body problem admits noncollision singularities.[7][8]

Development

Edvard Hugo von Zeipel proved in 1908 that if there is a collision singularity, then [math]\displaystyle{ J(\mathbf{q}(t)) }[/math] tends to a definite limit as [math]\displaystyle{ t\rightarrow t^* }[/math], where [math]\displaystyle{ J(\mathbf{q})=\sum_i m_i |\mathbf{q}_i|^2 }[/math] is the moment of inertia.[9] This implies that a necessary condition for a noncollision singularity is that the velocity of at least one particle becomes unbounded (since the positions [math]\displaystyle{ \mathbf{q} }[/math] remain finite up to this point).[1]

Mather and McGehee managed to prove in 1975 that a noncollision singularity can occur in the co-linear 4-body problem (that is, with all bodies on a line), but only after an infinite number of (regularized) binary collisions.[10]

Donald G. Saari proved in 1977 that for almost all (in the sense of Lebesgue measure) initial conditions in the plane or space for 2, 3 and 4-body problems there are singularity-free solutions.[11]

In 1984, Joe Gerver gave an argument for a noncollision singularity in the planar 5-body problem with no collisions.[12] He later found a proof for the 3n body case.[13]

Finally, in his 1988 doctoral dissertation, Jeff Xia demonstrated a 5-body configuration that experiences a noncollision singularity.[3][4]

Joe Gerver has given a heuristic model for the existence of 4-body singularities.[14]

In his 2013 doctoral thesis at University of Maryland, Jinxin Xue considered a simplified model for the planar four-body problem case of the Painlevé conjecture. Based on a model of Gerver, he proved that there is a Cantor set of initial conditions which lead to solutions of the Hamiltonian system whose velocities are accelerated to infinity within finite time avoiding all earlier collisions. In 2014, Xue extended his previous work and proved the conjecture for n=4.[15][5][6]

References

  1. ↑ 1.0 1.1 Diacu, Florin N. (1993). "Painlevé's Conjecture". The Mathematical Intelligencer 13 (2). 
  2. ↑ Diacu, Florin; Holmes, Philip (1996). Celestial Encounters: The Origins of Chaos and Stability. Princeton University Press. ISBN 0-691-02743-9. 
  3. ↑ 3.0 3.1 Xia, Zhihong (1992). "The Existence of Noncollision Singularities in Newtonian Systems". Annals of Mathematics. Second Series 135 (3): 411–468. doi:10.2307/2946572. 
  4. ↑ 4.0 4.1 Saari, Donald G.; Xia, Zhihong (Jeff) (1993). "Off to Infinity in Finite Time". Notices of the AMS 42 (5): 538–546. 
  5. ↑ 5.0 5.1 Xue, Jinxin (2014). "Noncollision Singularities in a Planar Four-body Problem". arXiv:1409.0048 [math.DS].
  6. ↑ 6.0 6.1 Xue, Jinxin (2020). "Non-collision singularities in a planar 4-body problem". Acta Mathematica 224 (2): 253–388. doi:10.4310/ACTA.2020.v224.n2.a2. 
  7. ↑ Painlevé, P. (1897). Lecons sur la théorie analytique des équations différentielles. Paris: Hermann. https://archive.org/details/leonssurlathorie00pain. 
  8. ↑ Oeuvres de Paul Painlevé. Tome I. Paris: Ed. Centr. Nat. Rech. Sci.. 1972. 
  9. ↑ von Zeipel, H. (1908). "Sur les singularités du problème des corps". Arkiv för Matematik, Astronomi och Fysik 4: 1–4. 
  10. ↑ Mather, J.; McGehee, R. (1975). "Solutions of the collinear four-body problem which become unbounded in finite time". in Moser, J.. Dynamical Systems Theory and Applications. Berlin: Springer-Verlag. pp. 573–589. ISBN 3-540-07171-7. https://archive.org/details/dynamicalsystems00mose. 
  11. ↑ Saari, Donald G. (1977). "A global existence theorem for the four-body problem of Newtonian mechanics". J. Differential Equations 26 (1): 80–111. doi:10.1016/0022-0396(77)90100-0. Bibcode: 1977JDE....26...80S. 
  12. ↑ Gerver, J. L. (1984). "A possible model for a singularity without collisions in the five-body problem". J. Diff. Eq. 52 (1): 76–90. doi:10.1016/0022-0396(84)90136-0. Bibcode: 1984JDE....52...76G. 
  13. ↑ Gerver, J. L. (1991). "The existence of pseudocollisions in the plane". J. Diff. Eq. 89 (1): 1–68. doi:10.1016/0022-0396(91)90110-U. Bibcode: 1991JDE....89....1G. 
  14. ↑ Gerver, Joseph L. (2003). "Noncollision Singularities: Do Four Bodies Suffice?". Exp. Math. 12 (2): 187–198. doi:10.1080/10586458.2003.10504491. http://projecteuclid.org/euclid.em/1067634730. 
  15. ↑ Xue, J.; Dolgopyat, D. (2016). "Non-Collision Singularities in the Planar Two-Center-Two-Body Problem". Commun. Math. Phys. 345 (3): 797–879. doi:10.1007/s00220-016-2688-6. Bibcode: 2016CMaPh.345..797X. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Painlevé_conjecture&oldid=3278553"