Physics:Rankine half body
This article includes a list of references, related reading or external links, but its sources remain unclear because it lacks inline citations. (November 2016) (Learn how and when to remove this template message) |

In the field of fluid dynamics, a Rankine half body is a feature of fluid flow discovered by Scottish physicist and engineer William Rankine that is formed when a fluid source is added to a fluid undergoing potential flow. Superposition of uniform flow and source flow yields the Rankine half body flow. A practical example of this type of flow is a bridge pier or a strut placed in a uniform stream. The resulting stream function () and velocity potential () are obtained by simply adding the stream function and velocity potential for each individual flow.
Solution
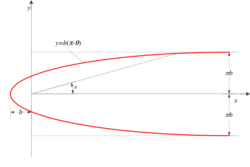
The flow equations of the Rankine half body are solved using the principle of superposition, combining the solutions of the linear flow of the stream and the circular flow of the source.
Given the linear flow field and the source , we have
The stagnation point for this flow can be determined by equating the velocity to zero in either directions. Because of symmetry of flow in y-direction, stagnation point must lie on x-axis.
Equating both and to zero, we obtain .
At and we have stagnation points.
Now, we note that , so following this constant streamline gives the outline of the body:
Then, describes the half body outline.
The resultant velocity at any point is
If we evaluate the velocities along the upper surface, we find a maximum value of 1.26U at θ=63°. Beyond this point the surface flow decelerates and pressure increases causing flow separation.[1]
Significance
This type of flow provides important information about flow in front part of streamlined body. It is probable that at the boundary, flow is not properly represented for real flow. The pressure and velocity of flow near to boundary layer is calculated by applying the Bernoulli's principle and is approximated with potential flow. The above equations may be used to calculate the stress on the body placed into the flow stream.
See also
References
- ↑ White, Frank M. (2016). Fluid mechanics (8. ed.). New York, NY: McGraw-Hill. ISBN 978-0-07-339827-3.
- http://www.iust.ac.ir/files/mech/mazidi_9920c/fluid_ii/lecture8.pdf (pg no 22.23)
- http://www-mdp.eng.cam.ac.uk/web/library/enginfo/aerothermal_dvd_only/aero/fprops/poten/node35.html
- http://nptel.ac.in/courses/101103004/15
- http://poisson.me.dal.ca/site2/courses/mech3300/Superposition.pdf
- https://faculty.poly.edu/~rlevicky/Files/Other/Handout14_6333.pdf
- http://web.mit.edu/2.016/www/handouts/2005Reading4.pdf
- http://www1.maths.leeds.ac.uk/~kersale/2620/Notes/chapter_4.pdf
 |
