Physics:Rheonomous
A mechanical system is rheonomous if its equations of constraints contain the time as an explicit variable.[1][2] Such constraints are called rheonomic constraints. The opposite of rheonomous is scleronomous.[1][2]
Example: simple 2D pendulum

As shown at right, a simple pendulum is a system composed of a weight and a string. The string is attached at the top end to a pivot and at the bottom end to a weight. Being inextensible, the string has a constant length. Therefore, this system is scleronomous; it obeys the scleronomic constraint
- ,
where is the position of the weight and the length of the string.
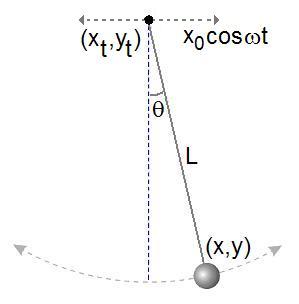
The situation changes if the pivot point is moving, e.g. undergoing a simple harmonic motion
- ,
where is the amplitude, the angular frequency, and time.
Although the top end of the string is not fixed, the length of this inextensible string is still a constant. The distance between the top end and the weight must stay the same. Therefore, this system is rheonomous; it obeys the rheonomic constraint
- .
See also
References
- ↑ 1.0 1.1 Goldstein, Herbert (1980). Classical Mechanics (2nd ed.). United States of America: Addison Wesley. p. 12. ISBN 0-201-02918-9. https://archive.org/details/classicalmechani00gold_639. "Constraints are further classified according as the equations of constraint contain the time as an explicit variable (rheonomous) or are not explicitly dependent on time (scleronomous)."
- ↑ 2.0 2.1 Spiegel, Murray R. (1994). Theory and Problems of THEORETICAL MECHANICS with an Introduction to Lagrange's Equations and Hamiltonian Theory. Schaum's Outline Series. McGraw Hill. p. 283. ISBN 0-07-060232-8. "In many mechanical systems of importance the time t does not enter explicitly in the equations (2) or (3). Such systems are sometimes called scleronomic. In others, as for example those involving moving constraints, the time t does enter explicitly. Such systems are called rheonomic."
 |
