Physics:Shepard tables

From HandWiki
Short description: Optical illusion
Shepard tables illusion, named for its creator Roger N. Shepard

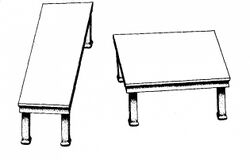
Shepard tables (also known as the Shepard tabletop illusion) are an optical illusion first published in 1990 as "Turning the Tables," by Stanford psychologist Roger N. Shepard in his book Mind Sights, a collection of illusions that he had created.[1] It is one of the most powerful optical illusions, typically creating length miscalculations of 20–25%.[2]

Roger Shepard, creator of the Shepard tables illusion

To quote A Dictionary of Psychology, the Shepard table illusion makes "a pair of identical parallelograms representing the tops of two tables appear radically different" because our eyes decode them according to rules for three-dimensional objects.[1]

This illusion is based on a drawing of two parallelograms, identical aside from a rotation of 90 degrees. When the parallelograms are presented as tabletops, however, we see them as objects in three-dimensional space. One "table" seems long and narrow, with its longer dimension receding into the distance. The other "table" looks almost square, because we interpret its shorter dimension as foreshortening.[3] The MIT Encyclopedia of the Cognitive Sciences explains the illusion as an effect of "size and shape constancy [which] subjectively expand[s] the near-far dimension along the line of sight."[4] It classifies Shepard tables as an example of a geometrical illusion, in the category of an "illusion of size."[4]

According to Shepard, "any knowledge or understanding of the illusion we may gain at the intellectual level remains virtually powerless to diminish the magnitude of the illusion."[5] Children diagnosed with autism spectrum disorder are less susceptible to the Shepard table illusion than typically developing children[2] but are equally susceptible to the Ebbinghaus illusion.[6]

Shepard had described an earlier, less-powerful version of the illusion in 1981 as the "parallelogram illusion" (Perceptual Organization, pp. 297–9).[1] The illusion can also be constructed using identical trapezoids rather than identical parallelograms.[7]

A variant of the Shepard tabletop illusion was named "Best Illusion of the Year" for 2009.[8][9]

Christopher W. Tyler, among others, has done scholarly research on the illusion.[10]

References

  1. ↑ 1.0 1.1 1.2 Colman, Andrew M. A Dictionary of Psychology (3 ed.). Oxford University Press. ISBN 9780191726828. http://www.oxfordreference.com/view/10.1093/oi/authority.20110803110312149?rskey=EtCz6d&result=1. "The illusion was first presented by the US psychologist Roger N(ewland) Shepard (born 1929) in his book Mind Sights: Original Visual Illusions, Ambiguities, and Other Anomalies (1990, p. 48). Shepard commented that ‘any knowledge or understanding of the illusion we may gain at the intellectual level remains virtually powerless to diminish the magnitude of the illusion’ (p. 128)." 
  2. ↑ 2.0 2.1 Chouinard, Philippe. "The Psychology of Seeing in Autism". La Trobe University. https://www.latrobe.edu.au/psychology/research/research-areas/cognitive-and-developmental-psychology/the-psychology-of-seeing-in-autism. "[The Shepard tables] illusion is one of the strongest optical illusions that exists, on average the apparent size difference is 20–25%. Our preliminary work and earlier work performed by others (Mitchell, Mottron, Soulieres, & Ropar, 2010) reveal how susceptibility to this particular illusion is diminished considerably in persons with an ASD." 
  3. ↑ Shapiro, Arthur Gilman; Todorovic, Dejan (2012). The Oxford Compendium of Visual Illusions. Oxford University Press. p. 239. ISBN 978-0199794607. https://books.google.com/books?id=bzfADgAAQBAJ&q=oxford+compendium+visual+illusions+shepard&pg=PA239. "For example, the famous Shepard tabletop illusion (Shepard, 1981) is more convincing when the planes are embedded in box shapes than when they are presented in isolation." 
  4. ↑ 4.0 4.1 Wilson, Robert Andrew; Keil, Frank C (2001). The MIT Encyclopedia of the Cognitive Sciences. MIT Press. pp. 385–386. ISBN 978-0262731447. https://books.google.com/books?id=-wt1aZrGXLYC. "size and shape constancy subjectively expand the near-far dimension along the line of sight to compensate for geometrical foreshortening." 
  5. ↑ Shepard, RN (1990). Mind Sights: Original visual illusions, ambiguities, and other anomalies, with a commentary on the play of mind in perception and art. W.H. Freeman and Company. p. 128. ISBN 978-0716721345. https://books.google.com/books?id=1vtlQgAACAAJ. "Because the inference about orientation, depth, and length are provided automatically by underlying neuronal machinery, any knowledge or understanding of the illusion we may gain at the intellectual level remains virtually powerless to diminish the magnitude of the illusion." 
  6. ↑ Landry, O.; Royals, K. (May 9, 2018). "Illusion Strength and Associated Eye Movements in Children with Autism Spectrum Disorder While Viewing Shepard and Ebbinghaus Illusion Displays". INSAR 2018 Annual Meeting. Rotterdam: International Society for Autism Research. https://insar.confex.com/insar/2018/webprogram/Paper28297.html. "The children with ASD (M = .14, SD = .10) were less susceptible to the Shepard’s tabletops illusion than the typically developing children (M = .20, SD = .05), t (28) = 2.41, p = .043." 
  7. ↑ Martinez-Conde, Susana; Macknik, Stephen (2017). Champions of Illusion: The Science Behind Mind-Boggling Images and Mystifying Brain Puzzles. Farrar, Straus and Giroux. p. 46. ISBN 978-0374120405. https://books.google.com/books?id=HuklDwAAQBAJ. "Photocopy this page and then ..cut around the trapezoid shapes…The effect is a version of the classic Shepard Tabletop illusion." 
  8. ↑ Phillips, David (October 14, 2009). "Shepard's tables – What's up?". OpticalIllusion.net. https://www.opticalillusion.net/optical-illusions/shepards-tables-whats-up/. "Recently Lydia Maniatis pointed out a puzzling aspect of the illusion, in her prize-winning entry for the Illusion of the Year Competition." 
  9. ↑ Maniatis, Lydia (2009). "Another turn: a variant on the Shepard tabletop illusion". Best Illusion of the Year Contest. http://illusionoftheyear.com/2009/05/another-turn-a-variant-on-the-shepard-tabletop-illusion/. "The three pink- and blue-colored parallelograms are the same. All blue lines are equal in length; all pink lines are also equal. Box B is simply Box C rotated counterclockwise. But the three parallelograms look different, and boxes B and C look different." 
  10. ↑ Tyler, Christopher W (May 19, 2011). "Paradoxical perception of surfaces in the Shepard tabletop illusion". i-Perception 3 (3): 137–141. doi:10.1068/i0422. PMID 23145230. "One of the most profound visual illusions .. is the Shepard tabletop illusion, in which the perspective view of two identical parallelograms as tabletops at different orientations gives a completely different sense of the aspect ratio of the implied rectangles in the two cases (Shepard 1990).". 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Shepard_tables&oldid=287914"