Physics:Squirmer
The squirmer is a model for a spherical microswimmer swimming in Stokes flow. The squirmer model was introduced by James Lighthill in 1952 and refined and used to model Paramecium by John Blake in 1971.[1] [2] Blake used the squirmer model to describe the flow generated by a carpet of beating short filaments called cilia on the surface of Paramecium. Today, the squirmer is a standard model for the study of self-propelled particles, such as Janus particles, in Stokes flow.[3]
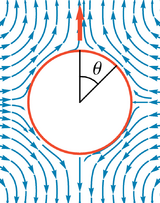
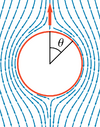
Velocity field in particle frame
Here we give the flow field of a squirmer in the case of a non-deformable axisymmetric spherical squirmer (radius [math]\displaystyle{ R }[/math]).[1][2] These expressions are given in a spherical coordinate system.
[math]\displaystyle{
u_r(r,\theta)=\frac 2 3 \left(\frac{R^3}{r^3} -1\right)B_1P_1(\cos\theta)+\sum_{n=2}^{\infty}\left(\frac{R^{n+2}}{r^{n+2}}-\frac{R^n}{r^n}\right)B_nP_n(\cos\theta)\;,
}[/math]
[math]\displaystyle{
u_{\theta}(r,\theta)=\frac 2 3 \left(\frac{R^3}{2r^3}+1\right)B_1V_1(\cos\theta)+\sum_{n=2}^{\infty}\frac 1 2\left(n\frac{R^{n+2}}{r^{n+2}}+(2-n)\frac{R^n}{r^n}\right)B_nV_n(\cos\theta)\;.
}[/math]
Here [math]\displaystyle{ B_n }[/math] are constant coefficients, [math]\displaystyle{ P_n(\cos\theta) }[/math] are Legendre polynomials, and [math]\displaystyle{ V_n(\cos\theta)=\frac{-2}{n(n+1)}\partial_{\theta}P_n(\cos\theta) }[/math].
One finds [math]\displaystyle{ P_1(\cos\theta)=\cos\theta, P_2(\cos\theta)=\tfrac 1 2 (3\cos^2\theta-1), \dots, V_1(\cos\theta)=\sin\theta, V_2(\cos\theta)= \tfrac{1}{2} \sin 2\theta, \dots }[/math].
The expressions above are in the frame of the moving particle. At the interface one finds [math]\displaystyle{ u_{\theta}(R,\theta)=\sum_{n=1}^{\infty} B_nV_n }[/math] and [math]\displaystyle{ u_r(R,\theta)=0 }[/math].
| Pusher, [math]\displaystyle{ \beta=-5 }[/math]|100px | Neutral, [math]\displaystyle{ \beta=0 }[/math]|100px | Puller, [math]\displaystyle{ \beta=5 }[/math]|100px | Shaker, [math]\displaystyle{ \beta=\infty }[/math]|100px | ||
| Pusher, [math]\displaystyle{ \beta=-5 }[/math]|100px | Neutral, [math]\displaystyle{ \beta=0 }[/math]|100px | Puller, [math]\displaystyle{ \beta=5 }[/math]|100px | Shaker, [math]\displaystyle{ \beta=\infty }[/math]|100px | ||
| Velocity field of squirmer and passive particle (top row: lab frame, bottom row: swimmer frame, [math]\displaystyle{ \beta = B_2/|B_1| }[/math] ). | |||||
Swimming speed and lab frame
By using the Lorentz Reciprocal Theorem, one finds the velocity vector of the particle [math]\displaystyle{ \mathbf{U}=-\tfrac{1}{2} \int \mathbf{u}(R,\theta)\sin\theta\mathrm{d}\theta=\tfrac 2 3 B_1 \mathbf{e}_z }[/math]. The flow in a fixed lab frame is given by [math]\displaystyle{ \mathbf{u}^L=\mathbf{u}+\mathbf{U} }[/math]:
[math]\displaystyle{
u_r^L(r,\theta)=\frac{R^3}{r^3}UP_1(\cos\theta)+\sum_{n=2}^{\infty}\left(\frac{R^{n+2}}{r^{n+2}}-\frac{R^n}{r^n}\right)B_nP_n(\cos\theta)\;,
}[/math]
[math]\displaystyle{
u_{\theta}^L(r,\theta)=\frac{R^3}{2r^3}UV_1(\cos\theta)+\sum_{n=2}^{\infty}\frac 1 2\left(n\frac{R^{n+2}}{r^{n+2}}+(2-n)\frac{R^n}{r^n}\right)B_nV_n(\cos\theta)\;.
}[/math]
with swimming speed [math]\displaystyle{ U=|\mathbf{U}| }[/math]. Note, that [math]\displaystyle{ \lim_{r\rightarrow\infty}\mathbf{u}^L=0 }[/math] and [math]\displaystyle{ u^L_r(R,\theta)\neq 0 }[/math].
Structure of the flow and squirmer parameter
The series above are often truncated at [math]\displaystyle{ n=2 }[/math] in the study of far field flow, [math]\displaystyle{ r\gg R }[/math]. Within that approximation, [math]\displaystyle{ u_{\theta}(R,\theta)=B_1\sin\theta+\tfrac 1 2 B_2 \sin 2 \theta }[/math], with squirmer parameter [math]\displaystyle{ \beta=B_2/|B_1| }[/math]. The first mode [math]\displaystyle{ n=1 }[/math] characterizes a hydrodynamic source dipole with decay [math]\displaystyle{ \propto 1/r^3 }[/math] (and with that the swimming speed [math]\displaystyle{ U }[/math]). The second mode [math]\displaystyle{ n=2 }[/math] corresponds to a hydrodynamic stresslet or force dipole with decay [math]\displaystyle{ \propto 1/r^2 }[/math].[4] Thus, [math]\displaystyle{ \beta }[/math] gives the ratio of both contributions and the direction of the force dipole. [math]\displaystyle{ \beta }[/math] is used to categorize microswimmers into pushers, pullers and neutral swimmers.[5]
| Swimmer Type | pusher | neutral swimmer | puller | shaker | passive particle |
| Squirmer Parameter | [math]\displaystyle{ \beta\lt 0 }[/math] | [math]\displaystyle{ \beta=0 }[/math] | [math]\displaystyle{ \beta\gt 0 }[/math] | [math]\displaystyle{ \beta=\pm\infty }[/math] | |
| Decay of Velocity Far Field | [math]\displaystyle{ \mathbf{u}\propto 1/r^2 }[/math] | [math]\displaystyle{ \mathbf{u}\propto 1/r^3 }[/math] | [math]\displaystyle{ \mathbf{u}\propto 1/r^2 }[/math] | [math]\displaystyle{ \mathbf{u}\propto 1/r^2 }[/math] | [math]\displaystyle{ \mathbf{u}\propto 1/r }[/math] |
| Biological Example | E.Coli | Paramecium | Chlamydomonas reinhardtii |
The above figures show the velocity field in the lab frame and in the particle-fixed frame. The hydrodynamic dipole and quadrupole fields of the squirmer model result from surface stresses, due to beating cilia on bacteria, or chemical reactions or thermal non-equilibrium on Janus particles. The squirmer is force-free. On the contrary, the velocity field of the passive particle results from an external force, its far-field corresponds to a "stokeslet" or hydrodynamic monopole. A force-free passive particle doesn't move and doesn't create any flow field.
See also
References
- ↑ Jump up to: 1.0 1.1 Lighthill, M. J. (1952). "On the squirming motion of nearly spherical deformable bodies through liquids at very small reynolds numbers". Communications on Pure and Applied Mathematics 5 (2): 109–118. doi:10.1002/cpa.3160050201. ISSN 0010-3640.
- ↑ Jump up to: 2.0 2.1 Blake, J. R. (1971). "A spherical envelope approach to ciliary propulsion". Journal of Fluid Mechanics 46 (1): 199–208. doi:10.1017/S002211207100048X. ISSN 0022-1120. Bibcode: 1971JFM....46..199B.
- ↑ Bickel, Thomas; Majee, Arghya; Würger, Alois (2013). "Flow pattern in the vicinity of self-propelling hot Janus particles". Physical Review E 88 (1): 012301. doi:10.1103/PhysRevE.88.012301. ISSN 1539-3755. PMID 23944457. Bibcode: 2013PhRvE..88a2301B.
- ↑ Happel, John; Brenner, Howard (1981). Low Reynolds number hydrodynamics. Mechanics of fluids and transport processes. 1. doi:10.1007/978-94-009-8352-6. ISBN 978-90-247-2877-0.
- ↑ Downton, Matthew T; Stark, Holger (2009). "Simulation of a model microswimmer". Journal of Physics: Condensed Matter 21 (20): 204101. doi:10.1088/0953-8984/21/20/204101. ISSN 0953-8984. PMID 21825510. Bibcode: 2009JPCM...21t4101D.
 |