Physics:Static light scattering
Static light scattering is a technique in physical chemistry that measures the intensity of the scattered light to obtain the average molecular weight Mw of a macromolecule like a polymer or a protein in solution. Measurement of the scattering intensity at many angles allows calculation of the root mean square radius, also called the radius of gyration Rg. By measuring the scattering intensity for many samples of various concentrations, the second virial coefficient, A2, can be calculated.[1][2][3][4][5]
Static light scattering is also commonly utilized to determine the size of particle suspensions in the sub-μm and supra-μm ranges, via the Lorenz-Mie (see Mie scattering) and Fraunhofer diffraction formalisms, respectively.
For static light scattering experiments, a high-intensity monochromatic light, usually a laser, is launched into a solution containing the macromolecules. One or many detectors are used to measure the scattering intensity at one or many angles. The angular dependence is required to obtain accurate measurements of both molar mass and size for all macromolecules of radius above 1–2% of the incident wavelength. Hence simultaneous measurements at several angles relative to the direction of the incident light, known as multi-angle light scattering (MALS) or multi-angle laser light scattering (MALLS), are generally regarded as the standard implementation of static light scattering. Additional details on the history and theory of MALS may be found in multi-angle light scattering.
To measure the average molecular weight directly without calibration from the light scattering intensity, the laser intensity, the quantum efficiency of the detector, and the full scattering volume and solid angle of the detector need to be known. Since this is impractical, all commercial instruments are calibrated using a strong, known scatterer like toluene since the Rayleigh ratio of toluene and a few other solvents were measured using an absolute light scattering instrument.
Theory
For a light scattering instrument composed of many detectors placed at various angles, all the detectors need to respond the same way. Usually, detectors will have slightly different quantum efficiency, different gains, and are looking at different geometrical scattering volumes. In this case, a normalization of the detectors is absolutely needed. To normalize the detectors, a measurement of a pure solvent is made first. Then an isotropic scatterer is added to the solvent. Since isotropic scatterers scatter the same intensity at any angle, the detector efficiency and gain can be normalized with this procedure. It is convenient to normalize all the detectors to the 90° angle detector.
where IR(90) is the scattering intensity measured for the Rayleigh scatterer by the 90° angle detector.
The most common equation to measure the weight-average molecular weight, Mw, is the Zimm equation[5] (the right-hand side of the Zimm equation is provided incorrectly in some texts, as noted by Hiemenz and Lodge):[6]
where
and
with
and the scattering vector for vertically polarized light is
with n0 the refractive index of the solvent, λ the wavelength of the light source, NA the Avogadro constant, c the solution concentration, and dn/dc the change in the refractive index of the solution with change in concentration. The intensity of the analyte measured at an angle is IA(θ). In these equations, the subscript A is for analyte (the solution) and T is for the toluene with the Rayleigh ratio of toluene, RT being 1.35×10−5 cm−1 for a HeNe laser. As described above, the radius of gyration, Rg, and the second virial coefficient, A2, are also calculated from this equation. The refractive index increment dn/dc characterizes the change of the refractive index n with the concentration c and can be measured with a differential refractometer.
A Zimm plot is built from a double extrapolation to zero angle and zero concentration from many angles and many concentration measurements. In its simplest form, the Zimm equation is reduced to:
for measurements made at low angle and infinite dilution since P(0) = 1.
There are typically several analyses developed to analyze the scattering of particles in solution to derive the above-named physical characteristics of particles. A simple static light scattering experiment entails the average intensity of the sample that is corrected for the scattering of the solvent will yield the Rayleigh ratio, R as a function of the angle or the wave vector q as follows:
Data analyses
Guinier plot
The scattered intensity can be plotted as a function of the angle to give information on the Rg which can simply be calculated using the Guinier approximation (developed by André Guinier) as follows:
where ln(ΔR(θ)) = lnP(θ) also known as the form factor with q = 4πn0sin(θ/2)/λ. Hence a plot of the corrected Rayleigh ratio, ΔR(θ) vs sin2(θ/2) or q2 will yield a slope Rg2/3. However, this approximation is only true for qRg < 1. Note that for a Guinier plot, the value of dn/dc and the concentration is not needed.
Kratky plot
The Kratky plot is typically used to analyze the conformation of proteins but can be used to analyze the random walk model of polymers. A Kratky plot can be made by plotting sin2(θ/2)ΔR(θ) vs sin(θ/2) or q2ΔR(θ) vs q.
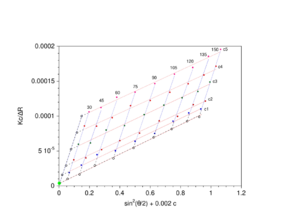
Zimm plot
For polymers and polymer complexes that are monodisperse () as determined by static light scattering, a Zimm plot is a conventional means of deriving the parameters such as Rg, molecular mass Mw and the second virial coefficient A2.
One must note that if the material constant K is not implemented, a Zimm plot will only yield Rg. Hence implementing K will yield the following equation:
The analysis performed with the Zimm plot uses a double-extrapolation to zero concentration and zero scattering angle resulting in a characteristic rhomboid plot. As the angular information is available, it is also possible to obtain the radius of gyration (Rg). Experiments are performed at several angles, which satisfy the condition and at least 4 concentrations. Performing a Zimm analysis on a single concentration is known as a partial Zimm analysis and is only valid for dilute solutions of strong point scatterers. The partial Zimm however, does not yield the second virial coefficient, due to the absence of the variable concentration of the sample. More specifically, the value of the second virial coefficient is either assumed to equal zero or is inputted as a known value in order to perform the partial Zimm analysis.
Debye plot

If the measured particles are smaller than λ/20, the form factor P(θ) can be neglected (P(θ)→1). Therefore, the Zimm equation is simplified to the Debye equation, as follows:
Note that this is also the result of an extrapolation to zero scattering angle. By acquiring data on concentration and scattering intensity, the Debye plot is constructed by plotting Kc/ΔR(θ) vs. concentration. The intercept of the fitted line gives the molecular mass, while the slope corresponds to the 2nd virial coefficient.
As the Debye plot is a simplification of the Zimm equation, the same limitations of the latter apply, i.e., samples should present a monodisperse nature. For polydisperse samples, the resulting molecular mass from a static light-scattering measurement will represent an average value. An advantage of the Debye plot is the possibility to determine the second virial coefficient. This parameter describes the interaction between particles and the solvent. In macromolecule solutions, for instance, it can assume negative (particle-particle interactions are favored), zero, or positive values (particle-solvent interactions are favored).[8]
Multiple scattering
Static light scattering assumes that each detected photon has only been scattered exactly once. Therefore, analysis according to the calculations stated above will only be correct if the sample has been diluted sufficiently to ensure that photons are not scattered multiple times by the sample before being detected. Accurate interpretation becomes exceedingly difficult for systems with non-negligible contributions from multiple scattering. In many commercial instruments where analysis of the scattering signal is automatically performed, the error may never be noticed by the user. Particularly for larger particles and those with high refractive index contrast, this limits the application of standard static light scattering to very low particle concentrations. On the other hand, for soluble macromolecules that exhibit a relatively low refractive index contrast versus the solvent, including most polymers and biomolecules in their respective solvents, multiple scattering is rarely a limiting factor even at concentrations that approach the limits of solubility.
However, as shown by Schaetzel,[9] it is possible to suppress multiple scattering in static light scattering experiments via a cross-correlation approach. The general idea is to isolate singly scattered light and suppress undesired contributions from multiple scattering in a static light scattering experiment. Different implementations of cross-correlation light scattering have been developed and applied. Currently, the most widely used scheme is the so-called 3D-dynamic light scattering method,.[10][11] The same method can also be used to correct dynamic light scattering data for multiple scattering contributions.[12]
Composition-gradient static light scattering
Samples that change their properties after dilution may not be analyzed via static light scattering in terms of the simple model presented here as the Zimm equation. A more sophisticated analysis known as 'composition-gradient static (or multi-angle) light scattering' (CG-SLS or CG-MALS) is an important class of methods to investigate protein–protein interactions, colligative properties, and other macromolecular interactions as it yields, in addition to size and molecular weight, information on the affinity and stoichiometry of molecular complexes formed by one or more associating macromolecular/biomolecular species. In particular, static light scattering from a dilution series may be analyzed to quantify self-association, reversible oligomerization, and non-specific attraction or repulsion, while static light scattering from mixtures of species may be analyzed to quantify hetero-association.[13]
Applications
One of the main applications of static light scattering for molecular mass determination is in the field of macromolecules, such as proteins and polymers,[14][15][16] as it is possible to measure the molecular mass of proteins without any assumption about their shape. Static light scattering is usually combined with other particle characterization techniques, such as size-exclusion chromatography (SEC), dynamic light scattering (DLS), and electrophoretic light scattering (ELS).
See also
- Differential static light scatter (DSLS)
- Dynamic light scattering (DLS)
- Single particle extinction and scattering (SPES)
- Light scattering
- Protein–protein interactions
References
- ↑ A. Einstein (1910). "Theorie der Opaleszenz von homogenen Flüssigkeiten und Flüssigkeitsgemischen in der Nähe des kritischen Zustandes". Annals of Physics 33 (16): 1275. doi:10.1002/andp.19103381612. Bibcode: 1910AnP...338.1275E. https://zenodo.org/record/1424187.
- ↑ C.V. Raman (1927). "Relation of Tyndall effect to osmotic pressure in colloidal solutions". Indian J. Phys. 2: 1.
- ↑ P.Debye (1944). "Light Scattering in Solutions". J. Appl. Phys. 15 (4): 338. doi:10.1063/1.1707436. Bibcode: 1944JAP....15..338D.
- ↑ B.H. Zimm (1945). "Molecular Theory of the Scattering of Light in Fluids". J. Chem. Phys. 13 (4): 141. doi:10.1063/1.1724013. Bibcode: 1945JChPh..13..141Z.
- ↑ 5.0 5.1 B.H. Zimm (1948). "The Scattering of Light and the Radial Distribution Function of High Polymer Solutions". J. Chem. Phys. 16 (12): 1093. doi:10.1063/1.1746738. Bibcode: 1948JChPh..16.1093Z.
- ↑ Hiemenz, Paul C.; Lodge, Timothy P. (2007). Polymer chemistry (2nd ed.). Boca Raton, Fla. [u.a.]: CRC Press. pp. 307–308. ISBN 978-1-57444-779-8.
- ↑ "Molecular mass measurement using static light scattering :: Anton Paar Wiki" (in en). https://wiki.anton-paar.com/en/molecular-mass-measurement-using-static-light-scattering/.
- ↑ Chang, Qing (2016), "Osmotic Pressure" (in en), Colloid and Interface Chemistry for Water Quality Control (Elsevier): pp. 37–47, doi:10.1016/b978-0-12-809315-3.00004-9, ISBN 978-0-12-809315-3, https://linkinghub.elsevier.com/retrieve/pii/B9780128093153000049, retrieved 2022-06-14
- ↑ Schaetzel, K. (1991). "Suppression of multiple-scattering by photon cross-correlation techniques". J. Mod. Opt. 38: SA393–SA398. doi:10.1088/0953-8984/2/S/062. Bibcode: 1990JPCM....2..393S.
- ↑ Urban, C.; Schurtenberger, P. (1998). "Characterization of turbid colloidal suspensions using light scattering techniques combined with cross-correlation methods". J. Colloid Interface Sci. 207 (1): 150–158. doi:10.1006/jcis.1998.5769. PMID 9778402. Bibcode: 1998JCIS..207..150U.
- ↑ Block, I.; Scheffold, F. (2010). "Modulated 3D cross-correlation light scattering: Improving turbid sample characterization". Review of Scientific Instruments 81 (12): 123107–123107–7. doi:10.1063/1.3518961. PMID 21198014. Bibcode: 2010RScI...81l3107B.
- ↑ Pusey, P.N. (1999). "Suppression of multiple scattering by photon cross-correlation techniques". Current Opinion in Colloid & Interface Science 4 (3): 177–185. doi:10.1016/S1359-0294(99)00036-9.
- ↑ Some, D. (2013). "Light Scattering Based Analysis of Biomolecular Interactions". Biophys. Rev. 5 (2): 147–158. doi:10.1007/s12551-013-0107-1. PMID 23646069.
- ↑ Sedlák, Marián (2006-03-01). "Large-Scale Supramolecular Structure in Solutions of Low Molar Mass Compounds and Mixtures of Liquids: I. Light Scattering Characterization" (in en). The Journal of Physical Chemistry B 110 (9): 4329–4338. doi:10.1021/jp0569335. ISSN 1520-6106. PMID 16509731. https://pubs.acs.org/doi/10.1021/jp0569335.
- ↑ Díaz‐Lasprilla, Ana M.; Mercado, Ronald A.; Ramírez‐Caballero, Gustavo E. (2021-06-20). "Glycerol polymerization degree effect on the emulsifying properties of polyglycerol esters" (in en). Journal of Applied Polymer Science 138 (24). doi:10.1002/app.50566. ISSN 0021-8995. https://onlinelibrary.wiley.com/doi/10.1002/app.50566.
- ↑ "Dimerization of Bovine Serum Albumin As Evidenced By Particle Size and Molecular Mass Measurement :: Anton-Paar.com" (in en). https://www.anton-paar.com/corp-en/services-support/document-finder/application-reports/dimerization-of-bovine-serum-albumin-as-evidenced-by-particle-size-and-molecular-mass-measurement/.
External links
 |
