Physics:Time-domain holography

From HandWiki

The time-domain counterpart of spatial holography is called time-domain holography. In other words, the principles of spatial holography is surveyed in time domain. Time-domain holography was inspired by the theory known as space-time duality which was introduced by Brian H. Kolner in 1994.

History

Holography was invented in 1948 by D. Gabor for increasing the resolution of electron microscope. Even though his idea didn't get much attention because of the lack of a light source with a long coherent length, but after invention of the laser, it became an important and applicable method of coding. In 1969 S. A. Akhmanov, pointed out the mathematical duality between the equations of paraxial (Fresnel) diffraction and narrow-band dispersion In his article "NONSTATIONARY PHENOMENA AND SPACE-TIME ANALOGY IN NONLINEAR OPTICS", which was about the second and third order nonlinear optical interactions. Finally, in 1994 Brian H. Kolner described this duality in detail in his "Space-Time Duality and the Theory of Temporal Imaging" article.

Space-time duality

The space-time duality establishes a direct relationship between the problems of paraxial diffraction and narrow-band dispersion. The electronic or magnetic equation of wave is constructed from the Maxwell's equation. For obtaining a general solution, the space-time evolution of an arbitrary waveform should be described, which is a hard task. Therefore, approximations are made in space or time domain. In other words, the space and time domain are treated individually by decreasing as much as possible the other domain's variations.

In space-domain, the wave is considered a monochrome, therefore it only has harmonic time variations (and the paraxial approximation) is considered as well. By solving the problem with the mentioned approximations a parabolic partial differential equation (PDE) is obtained for paraxial diffraction. In time-domain, a narrow band pulse is considered with an infinite plane wavefront. Using the mentioned approximations for narrow-band dispersion results in a parabolic partial differential equation.[1] This duality can also be observed by plotting them in spatial and time frequency. For example, the paraxial diffraction in time frequency and narrow-band dispersion in spatial frequency are both delta functions. Describing the holography in time domain, opened door to new opportunities and applications. Particularly in coherent high-speed optical telecommunications.

Principles of time-domain holography

For consistency, time-domain holography steps are referred to as the "recording process" and the "reconstruction process", even though they may not be the same as their spatial steps. Time-domain holography can be implement in: (1) an electro-optical approach and (2) an all-optical approach.[2]

Electro-optical approach

In the recording step, the complex amplitude information signal superposes with the reference signal (a continuous signal) in the optical coupler. In fact, the recording results is obtained at the exit of optical coupler. Then, a photo-diode takes this intensity and converts it to a current.

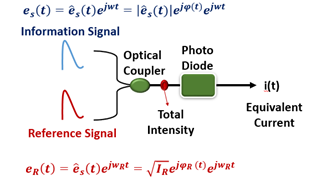
Recording step of time-domain holography

In the reconstruction step, the same reference signal enters the MachZehnder modulator (MZM), which is driven by a voltage v(t) proportional to the recorded intensity. In exact analogy with its spatial-domain counterpart the generated optical signal is composed of: (1) DC signal (2) Information Signal and (3) Conjugate of information signal.[3] It is noteworthy to mention that the conjugate of a signal can be used for impairment compensation.

Reconstruction step in electro-optical approach

All-optical approach

The recording process is the same in both approaches. In all-optical approach no photo-diode is used, instead the resulting intensity is used as a pump in the Cross-Phase Modulation (XPM) process, which takes place in a highly nonlinear fiber (HNLF). MZM is not used as well. Simply put, Amplitude modulation of reference signal takes place in electro-optical reconstruction whereas phase modulation takes place in all-optical reconstruction.[4]

Applications

Since time-domain holography allows the treatment of complex optical temporal information by using amplitude-only or phase-only-based modulation, any application requiring managing of complex-envelope signals can be significantly simplified with this approach.

Three general applications are as follows:

Generation of complex temporal signal or its conjugate

The temporal hologram can be numerically designed by using a computer. By giving its results to an arbitrary waveform generator (AWG), an amplitude-only signal is generated which interferes with the reference signal in MZM and the signals are generated in the output. By placing a Band-Pass Filter we can get the desired signal. In short, by creating the temporal hologram numerically, the signal is generated in the circuit.[5]

Three-dimensional storage

In spatial volume holograms, by using Bragg's formula, different holograms could be stored in one medium either in a constant angle and different wavelengths or by keeping the wavelengths constant and changing the angle. In the time domain, this medium can be partitioned into smaller parts and therefore a greater amount of information can be stored in it. This is obtained by giving a delay time between the object and the reference wave. By varying the delay time between the waves, they interfere in different longitudinal coordinates so the information is stored in different coordinates.[6]

Phase imaging

High-resolution amplitude and phase imaging can be obtained by using terahertz Pulse Time-Domain Holography (THz PTDH). The recording is done experimentally whereas the reconstruction can be done numerically. In this setup part of the femtosecond pulse is used as a probe, the other one is converted to THz pulse and by passing the object, the electrical field in the time domain is detected and recorded. By getting a Fourier-Transform THz spectra at every point of the wavefront is obtained (phase information is obtained). For reconstruction, this field should propagates to the object field. It is done by using the Transfer Function of Free Space. In other words, this part is done mathematically.[7]

Time-domain holography has several advantages compared with time-domain spectroscopy such as:

  1. PTDH is realized in a collimated beam, which means that the object can be stationary placed at any position inside it.
  2.  Since after the beam is collimated, it goes straight to the detection stage, the reconstruction quality does not depend on optics used in the layout.
  3.  It is faster.
  4.  The achievable resolution is higher.

The disadvantage of PTDH compared to TDS is its higher signal-to-noise ratio.[8]

References

  1. ↑ B. Kolner, "Space-time duality and the theory of temporal imaging," IEEE Journal of Quantum Electronics, vol. 30, no. 8, 1994.
  2. ↑ M. d. R. F. Ruiz, TIME- AND SPECTRAL-DOMAIN HOLOGRAPHY FOR HIGH-SPEED PROCESSING OF OPTICAL SIGNALS, 2016.
  3. ↑ Fernández-Ruiz, M. R.; Li, M.; Azaña, J. (September 2012). "Time-domain holography". IEEE Photonics Conference 2012. pp. 658–659. doi:10.1109/IPCon.2012.6358793. ISBN 978-1-4577-0733-9. https://ieeexplore.ieee.org/document/6358793. 
  4. ↑ M. d. R. F. Ruiz, TIME- AND SPECTRAL-DOMAIN HOLOGRAPHY FOR HIGH-SPEED PROCESSING OF OPTICAL SIGNALS, 2016.
  5. ↑ M. R. Fernández-Ruiz and J. Azaña, "Time-domain holograms for high-speed optical signal generation and processing," 2014.
  6. ↑ F. Yu and S. Yin, "Space-Time Processing with Photorefractive Volume Holography Using Femtosecond Laser Pulses," in Photorefractive Optics: Materials, Properties, and Applications, 2000.
  7. ↑ Petrov, Nikolay V.; Kulya, Maxim S.; Tsypkin, Anton N.; Bespalov, Victor G.; Gorodetsky, Andrei (May 2016). "Application of Terahertz Pulse Time-Domain Holography for Phase Imaging". IEEE Transactions on Terahertz Science and Technology 6 (3): 464–472. doi:10.1109/TTHZ.2016.2530938. ISSN 2156-342X. https://www.researchgate.net/publication/301240194. 
  8. ↑ Petrov, Nikolay V.; Gorodetsky, Andrei A.; Bespalov, Victor G. (2013). "Holography and phase retrieval in terahertz imaging". Proceedings of SPIE. Terahertz Emitters, Receivers, and Applications IV 8846: 88460S. doi:10.1117/12.2023918. ISSN 0277-786X. Bibcode: 2013SPIE.8846E..0SP. https://www.researchgate.net/publication/259183907. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Time-domain_holography&oldid=3276984"