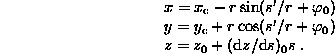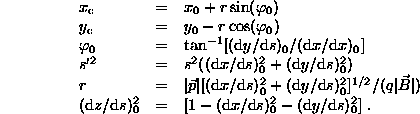Physics:Trajectory of a charged particle

The trajectory of a charged particle can be calculated from the equations of motion. Neglecting radiative corrections (see Jackson75) and in the absence of an electric field, the equation has the simple geometrical form:

For details and units Equations of Motion.

The integral of this second-order differential equation depends on six initial values. Assuming an s₀ on a reference surface (e.g. a plane z = const.), the trajectory is determined by five parameters, e.g. x, y, , and in the reference plane.

For constant the solution of the equations is a helix. Choosing , one obtains

, define the position of the axis of the helix (its ``centre), s is the projected path length, r is the radius of the projection of the helix. We have

In the ``bubble chamber convention the dip angle is defined by , hence

Other approximate explicit solutions for the trajectories of particles can be obtained using field symmetries allowing a simple expansion of the magnetic field, e.g. in accelerator theory. In other cases, an approximate expansion of the deviations of the field from an average value can give sufficiently precise correction formulae (e.g. in large detectors with near-homegeneous field, or in polarized targets, see Bradamante77). Trajectories in quadrupole fields allow a particularly elegant explicit solution ( Quadrupole Magnet).

For numerical solutions to the equations of the trajectory in a non-homogeneous field see Bock98 on numerical integration, Runge-Kutta methods, predictor-corrector methods, Numerov's method.

In many cases it is sufficient to know the intersection point of a particle trajectory with only few detector planes, without reference to the track behaviour elsewhere. The intersection coordinates can be expressed in terms of the initial track parameters

and one can try to parameterize the function . For more details and references see Eichinger81.