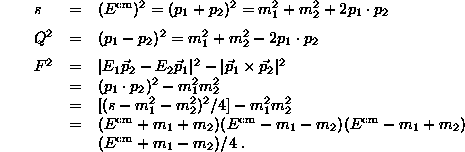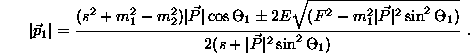Physics:Two-body kinematics

Given two four-momenta . There are two one-particle Lorentz invariants, the squares of the masses

and one two-particle invariant

From these, other Lorentz invariants can be formed such as

, often denoted E^*, is the total energy in the ``centre-of-mass reference system defined by . is also the ``effective mass of the two-particle system. Q² is most interesting when one of the particles is incoming and the other outgoing, in a collision process. It is called the momentum transfer and also denoted t. F is called Möller's invariant flux factor; it is given by the area (with respect to the Minkovski metric) of the parallelogram spanned by the two four-momenta p₁ and p₂.

If particle 2 is the target particle at rest, in a collision, i.e. , its rest system is called the laboratory system. We have

where

If the total four-momentum is given, in an arbitrary reference system, the velocity of the centre-of-mass system is

Then lies on an ellipsoid with principal half axes , and , and with the centre at , where

Define the angles and by

The polar equation for the ellipsoid is

In the special case one solution is and the other solution is given by

If in addition m₁ = m₂, then

This relation applies to the final state in elastic scattering for two particles with equal masses, and one particle at rest in the initial state.  also Mandelstam Variables also Mandelstam Variables and Barnett96.