Physics:Willam-Warnke yield criterion
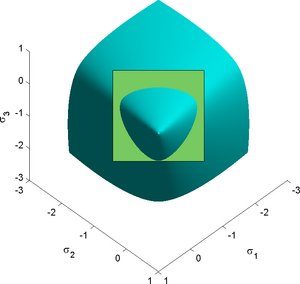
The Willam-Warnke yield criterion [1] is a function that is used to predict when failure will occur in concrete and other cohesive-frictional materials such as rock, soil, and ceramics. This yield criterion has the functional form
where is the first invariant of the Cauchy stress tensor, and are the second and third invariants of the deviatoric part of the Cauchy stress tensor. There are three material parameters ( - the uniaxial compressive strength, - the uniaxial tensile strength, - the equibiaxial compressive strength) that have to be determined before the Willam-Warnke yield criterion may be applied to predict failure.
In terms of , the Willam-Warnke yield criterion can be expressed as
where is a function that depends on and the three material parameters and depends only on the material parameters. The function can be interpreted as the friction angle which depends on the Lode angle (). The quantity is interpreted as a cohesion pressure. The Willam-Warnke yield criterion may therefore be viewed as a combination of the Mohr-Coulomb and the Drucker-Prager yield criteria.
Willam-Warnke yield function
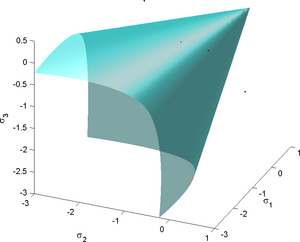

In the original paper, the three-parameter Willam-Warnke yield function was expressed as
where is the first invariant of the stress tensor, is the second invariant of the deviatoric part of the stress tensor, is the yield stress in uniaxial compression, and is the Lode angle given by
The locus of the boundary of the stress surface in the deviatoric stress plane is expressed in polar coordinates by the quantity which is given by
where
The quantities and describe the position vectors at the locations and can be expressed in terms of as (here is the failure stress under equi-biaxial compression and is the failure stress under uniaxial tension)
The parameter in the model is given by
The Haigh-Westergaard representation of the Willam-Warnke yield condition can be written as
where
Modified forms of the Willam-Warnke yield criterion

An alternative form of the Willam-Warnke yield criterion in Haigh-Westergaard coordinates is the Ulm-Coussy-Bazant form:[2]
where
and
The quantities are interpreted as friction coefficients. For the yield surface to be convex, the Willam-Warnke yield criterion requires that and .
See also
References
- ↑ Willam, K. J. and Warnke, E. P. (1975). Constitutive models for the triaxial behavior of concrete. Proceedings of the International Assoc. for Bridge and Structural Engineering , vol 19, pp. 1- 30.
- ↑ Ulm, F-J., Coussy, O., Bazant, Z. (1999) The ‘‘Chunnel’’ Fire. I: Chemoplastic softening in rapidly heated concrete. ASCE Journal of Engineering Mechanics, vol. 125, no. 3, pp. 272-282.
- Chen, W. F. (1982). Plasticity in Reinforced Concrete. McGraw Hill. New York.
External links
- Kaspar Willam and E.P. Warnke (1974). Constitutive model for the triaxial behavior of concrete
- Palko, J. L. (1993). Interactive reliability model for whisker-toughened ceramics
- The ‘‘Chunnel’’ Fire. I: Chemoplastic softening in rapidly heated concrete by Franz-Josef Ulm, Olivier Coussy, and Zdeneˇk P. Bazˇant.


