Pinched torus
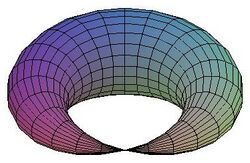
In mathematics, and especially topology and differential geometry, a pinched torus (or croissant surface) is a kind of two-dimensional surface. It gets its name from its resemblance to a torus that has been pinched at a single point. A pinched torus is an example of an orientable, compact 2-dimensional pseudomanifold.[1]
Parametrisation
A pinched torus is easily parametrisable. Let us write g(x,y) = 2 + sin(x/2).cos(y). An example of such a parametrisation − which was used to plot the picture − is given by ƒ : [0,2π)2 → R3 where:
- [math]\displaystyle{ f(x,y) = \left( g(x,y)\cos x , g(x,y)\sin x , \sin\!\left(\frac{x}{2}\right)\sin y \right) }[/math]
Topology
Topologically, the pinched torus is homotopy equivalent to the wedge of a sphere and a circle.[2][3] It is homeomorphic to a sphere with two distinct points being identified.[2][3]
Homology
Let P denote the pinched torus. The homology groups of P over the integers can be calculated. They are given by:
- [math]\displaystyle{ H_0(P,\Z) \cong \Z, \ H_1(P,\Z) \cong \Z, \ \text{and} \ H_2(P,\Z) \cong \Z. }[/math]
Cohomology
The cohomology groups of P over the integers can be calculated. They are given by:
- [math]\displaystyle{ H^0(P,\Z) \cong \Z, \ H^1(P,\Z) \cong \Z, \ \text{and} \ H^2(P,\Z) \cong \Z. }[/math]
References
- ↑ Brasselet, J. P. (1996). "Intersection of Algebraic Cycles". Journal of Mathematical Sciences (Springer New York) 82 (5): 3625–3632. doi:10.1007/bf02362566.
- ↑ 2.0 2.1 Hatcher, Allen (2001), Algebraic Topology, Cambridge University Press, ISBN 0-521-79540-0
- ↑ 3.0 3.1 Allen Hatcher. "Chapter 0: Algebraic Topology". http://www.math.cornell.edu/~hatcher/AT/ATch0.pdf. Retrieved August 6, 2010.
 |  |
