Pipelining (DSP implementation)
Pipelining is an important technique used in several applications such as digital signal processing (DSP) systems, microprocessors, etc. It originates from the idea of a water pipe with continuous water sent in without waiting for the water in the pipe to come out. Accordingly, it results in speed enhancement for the critical path in most DSP systems. For example, it can either increase the clock speed or reduce the power consumption at the same speed in a DSP system.
Concept
Pipelining allows different functional units of a system to run concurrently. Consider an informal example in the following figure. A system includes three sub-function units (F0, F1 and F2). Assume that there are three independent tasks (T0, T1 and T2) being performed by these three function units. The time for each function unit to complete a task is the same and will occupy a slot in the schedule.
If we put these three units and tasks in a sequential order, the required time to complete them is five slots.
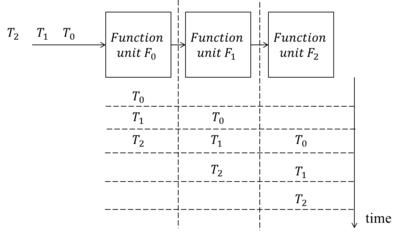
However, if we pipeline T0 to T2 concurrently, the aggregate time is reduced to three slots.
Therefore, it is possible for an adequate pipelined design to achieve significant enhancement on speed.
Costs and disadvantages
Pipelining cannot decrease the processing time required for a single task. The advantage of pipelining is that it increases the throughput of the system when processing a stream of tasks.
Applying too many pipelined functions can lead to increased latency - that is, the time required for a single task to propagate through the full pipe is prolonged. A pipelined system may also require more resources (buffers, circuits, processing units, memory etc.), if the reuse of resources across different stages is restricted.
Comparison with parallel approaches
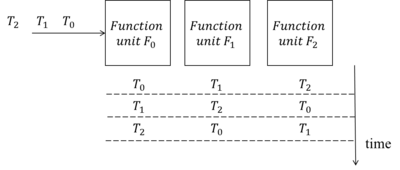
Another technique to enhance the efficiency through concurrency is parallel processing. The core difference is that parallel techniques usually duplicate function units and distribute multiple input tasks at once amongst them. Therefore, it can complete more tasks per unit time but may suffer more expensive resource costs.
For the previous example, the parallel technique duplicates each function units into another two. Accordingly, all the tasks can be operated upon by the duplicated function units with the same function simultaneously. The time to complete these three tasks is reduced to three slots.
Pipelining in FIR filters
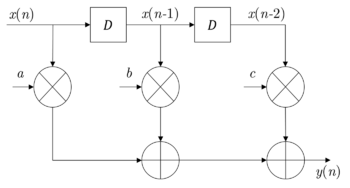
Consider a 3-tap FIR filter:[1]
- [math]\displaystyle{ y(n)=ax(n)+bx(n-1)+cx(n-2) }[/math]
which is as shown in the following figure.
Assume the calculation time for multiplication units is Tm and Ta for add units. The critical path, representing the minimum time required for processing a new sample, is limited by 1 multiplication and 2 add function units. Therefore, the sample period is given by
- [math]\displaystyle{ T_\text{sample} \ge T_m + 2T_a }[/math]
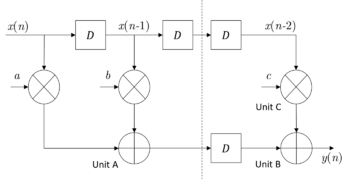
However, such structure may not be suitable for the design with the requirement of high speed. To reduce the sampling period, we can introduce extra pipelining registers along the critical data path. Then the structure is partitioned into two stages and the data produced in the first stage will be stored in the introduced registers, delaying one clock to the second stage. The data in first three clocks is recorded in the following table. Under such pipelined structure, the sample period is reduced to
- [math]\displaystyle{ T_\text{sample} \ge T_m + T_a. }[/math]
Pipelining in 1st-order IIR filters
By combining look-ahead techniques and pipelining,[2] we are able to enhance the sample rate of target design. Look-ahead pipelining will add canceling poles and zeroes to the transfer function such that the coefficients of the following terms in the denominator of the transfer function are zero.
- [math]\displaystyle{ \{z^{-1},\ldots,z^{-(M-1)}\} }[/math]
Then, the output sample y(n) can be computed in terms of the inputs and the output sample y(n − M) such that there are M delay elements in the critical loop. These elements are then used to pipeline the critical loop by M stages so that the sample rate can be increased by a factor M.
Consider the 1st-order IIR filter transfer function
- [math]\displaystyle{ H(z)=\frac{1}{1-az^{-1}} }[/math]
The output y(n) can be computed in terms of the input u(n) and the previous output.
- [math]\displaystyle{ y(n) = ay(n-1) + u(n) }[/math]
In a straightforward structure to design such function, the sample rate of this recursive filter is restricted by the calculation time of one multiply-add operation.
To pipeline such design, we observe that H has a pole at
- [math]\displaystyle{ z=a, a\le1 }[/math]
Therefore, in a 3-stage pipelined equivalent stable filter, the transfer function can be derived by adding poles and zeros at
- [math]\displaystyle{ z=ae^{\pm(\frac{2j\pi}{3})} }[/math]
and is given by
- [math]\displaystyle{ H(z)=\frac{1+az^{-1}+a^2 z^{-2}}{1-a^3 z^{-3}} }[/math]
Therefore, the corresponding sample rate can be increased by a factor 3.
Other examples of pipelined DSP systems
- Pipelined Walsh–Fourier transform[3]
- Pipelined unitary transforms[4]
- Pipelined DFT[5]
- Pipelined FFT[6]
References
- ↑ Keshab K. Parhi, VLSI Digital Signal Processing Systems: Design and Implementation, John Wiley, 1999
- ↑ Slides for VLSI Digital Signal Processing Systems: Design and Implementation John Wiley & Sons, 1999 (ISBN: 0-471-24186-5): http://www.ece.umn.edu/users/parhi/SLIDES/chap10.pdf
- ↑ M. R. Ashouri and Anthony G. Constantinides, "A pipeline fast Walsh Fourier transform," in Proc. IEEE Int. Conf. ASSP Hartford, CT, May 9–11), pp. 515-518, 1977.
- ↑ Fino, B.J.; Algazi, V.R.; , "Parallel and pipeline computation of fast unitary transforms," Electronics Letters , vol.11, no.5, pp.93-94, March 6, 1975
- ↑ Tzou, K.-H.; Morgan, N.P.; , "A fast pipelined DFT processor and its programming consideration," Electronic Circuits and Systems, IEE Proceedings G , vol.132, no.6, pp.273-276, December 1985
- ↑ H. L. Gorginsky and G. A. Works, "A pipeline fast Fourier transform," IEEE Trans. Comput., vol. C-19, pp. 1015-1019, Nov. 1970.
 |  |
