Rademacher system

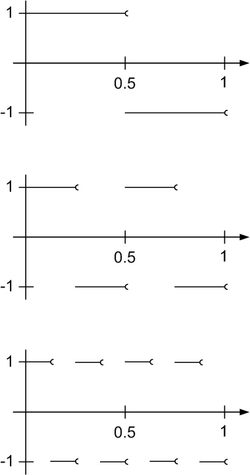
In mathematics, in particular in functional analysis, the Rademacher system, named after Hans Rademacher, is an incomplete orthogonal system of functions on the unit interval of the following form:

$\{t\mapsto r_n(t)=\mathrm{sgn}(\sin 2^{n+1}\pi t);t\in [0,1],n\in \mathbb{\mathbb{N}}\}.$

The Rademacher system is stochastically independent, and is closely related to the Walsh system. Specifically, the Walsh system can be constructed as a product of Rademacher functions.

To see that the Rademacher system is an incomplete orthogonal system and not an orthonormal basis, consider the function on the unit interval defined by the following equation:

$f(t)=4|x-\frac{1}{2}|-1$

This function is orthogonal to all the functions in the Rademacher system, yet is nonzero.

References

• Rademacher, Hans (1922). "Einige Sätze über Reihen von allgemeinen Orthogonalfunktionen". Math. Ann. 87 (1): 112–138. doi:10.1007/BF01458040. 
• Hazewinkel, Michiel, ed. (2001), "Orthogonal system", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Main_Page 
• Heil, Christopher E. (1997). "A basis theory primer". http://www.math.gatech.edu/~heil/papers/bases.pdf. 
• Curbera, Guillermo P. (2009). "How Summable are Rademacher Series?". Vector Measures, Integration and Related Topics. Basel: Birkhäuser Basel. pp. 135–148. doi:10.1007/978-3-0346-0211-2_13. ISBN 978-3-0346-0210-5. 

External links

• Rademacher system in the Encyclopedia of Mathematics