Regular paperfolding sequence

In mathematics the regular paperfolding sequence, also known as the dragon curve sequence, is an infinite sequence of 0s and 1s. It is obtained from the repeating partial sequence

1, ?, 0, ?, 1, ?, 0, ?, 1, ?, 0, ?, ...

by filling in the question marks by another copy of the whole sequence. The first few terms of the resulting sequence are:

1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, ... (sequence A014577 in the OEIS)

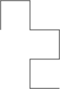
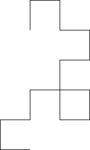
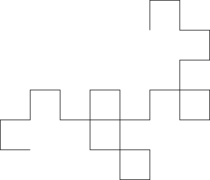
If a strip of paper is folded repeatedly in half in the same direction, [math]\displaystyle{ i }[/math] times, it will get [math]\displaystyle{ 2^i-1 }[/math] folds, whose direction (left or right) is given by the pattern of 0's and 1's in the first [math]\displaystyle{ 2^i-1 }[/math] terms of the regular paperfolding sequence. Opening out each fold to create a right-angled corner (or, equivalently, making a sequence of left and right turns through a regular grid, following the pattern of the paperfolding sequence) produces a sequence of polygonal chains that approaches the dragon curve fractal:

1	1 1 0	1 1 0 1 1 0 0	1 1 0 1 1 0 0 1 1 1 0 0 1 0 0	...

Properties

The value of any given term [math]\displaystyle{ t_n }[/math] in the regular paperfolding sequence, starting with [math]\displaystyle{ n=1 }[/math], can be found recursively as follows. Divide [math]\displaystyle{ n }[/math] by two, as many times as possible, to get a factorization of the form [math]\displaystyle{ n=m\cdot 2^k }[/math] where [math]\displaystyle{ m }[/math] is an odd number. Then [math]\displaystyle{ t_n = \begin{cases} 1 & \text{if } m \equiv 1 \mod 4 \\ 0 & \text{if } m \equiv 3 \mod 4 \end{cases} }[/math] Thus, for instance, [math]\displaystyle{ t_{12}=t_3=0 }[/math]: dividing 12 by two, twice, leaves the odd number 3. As another example, [math]\displaystyle{ t_{13}=1 }[/math] because 13 is congruent to 1 mod 4.

The paperfolding word 1101100111001001..., which is created by concatenating the terms of the regular paperfolding sequence, is a fixed point of the morphism or string substitution rules

11 → 1101

01 → 1001

10 → 1100

00 → 1000

as follows:

11 → 1101 → 11011001 → 1101100111001001 → 11011001110010011101100011001001 ...

It can be seen from the morphism rules that the paperfolding word contains at most three consecutive 0s and at most three consecutive 1s.

The paperfolding sequence also satisfies the symmetry relation:

[math]\displaystyle{ t_n = \begin{cases} 1 & \text{if } n = 2^k \\ 1-t_{2^k-n} & \text{if } 2^{k-1}\lt n\lt 2^k \end{cases} }[/math]

which shows that the paperfolding word can be constructed as the limit of another iterated process as follows:

1

1 1 0

110 1 100

1101100 1 1100100

110110011100100 1 110110001100100

In each iteration of this process, a 1 is placed at the end of the previous iteration's string, then this string is repeated in reverse order, replacing 0 by 1 and vice versa.

Generating function

The generating function of the paperfolding sequence is given by

[math]\displaystyle{ G(t_n;x)=\sum_{n=1}^{\infty}t_nx^n \, . }[/math]

From the construction of the paperfolding sequence, it can be seen that G satisfies the functional relation

[math]\displaystyle{ G(t_n;x) = G(t_n;x^2) + \sum_{n=0}^{\infty}x^{4n+1} = G(t_n;x^2) + \frac{x}{1-x^4} \, . }[/math]

Paperfolding constant

Substituting x = 0.5 into the generating function gives a real number between 0 and 1 whose binary expansion is the paperfolding word

[math]\displaystyle{ G(t_n;\frac{1}{2})=\sum_{n=1}^{\infty} \frac{t_n}{2^n} }[/math]

This number is known as the paperfolding constant and has the value

[math]\displaystyle{ \sum_{k=0}^{\infty} \frac {8^{2^k}}{2^{2^{k+2}}-1} = 0.85073618820186... }[/math] (sequence A143347 in the OEIS)

General paperfolding sequence

The regular paperfolding sequence corresponds to folding a strip of paper consistently in the same direction. If we allow the direction of the fold to vary at each step we obtain a more general class of sequences. Given a binary sequence (f_i), we can define a general paperfolding sequence with folding instructions (f_i).

For a binary word w, let w^‡ denote the reverse of the complement of w. Define an operator F_a as

[math]\displaystyle{ F_a : w \mapsto w a w^\ddagger \ }[/math]

and then define a sequence of words depending on the (f_i) by w₀ = ε,

[math]\displaystyle{ w_n = F_{f_1} ( F_{f_2} ( \cdots F_{f_n}(\varepsilon) \cdots ) ) \ . }[/math]

The limit w of the sequence w_n is a paperfolding sequence. The regular paperfolding sequence corresponds to the folding sequence f_i = 1 for all i.

If n = m·2^k where m is odd then

[math]\displaystyle{ t_n = \begin{cases} f_j & \text{if } m \equiv 1 \mod 4 \\ 1-f_j & \text{if } m \equiv 3 \mod 4 \end{cases} }[/math]

which may be used as a definition of a paperfolding sequence.

Properties

• A paperfolding sequence is not ultimately periodic.
• A paperfolding sequence is 2-automatic if and only if the folding sequence is ultimately periodic (1-automatic).

References

• Allouche, Jean-Paul; Shallit, Jeffrey (2003). Automatic Sequences: Theory, Applications, Generalizations. Cambridge University Press. ISBN 978-0-521-82332-6.