Retrieval Data Structure

In computer science, a retrieval data structure, also known as static function, is a space-efficient dictionary-like data type composed of a collection of (key, value) pairs that allows the following operations:

• Construction from a collection of (key, value) pairs
• Retrieve the value associated with the given key or anything if the key is not contained in the collection
• Update the value associated with a key (optional)

They can also be thought of as a function [math]\displaystyle{ b \colon \, \mathcal{U} \to \{0, 1\}^r }[/math] for a universe [math]\displaystyle{ \mathcal{U} }[/math] and the set of keys [math]\displaystyle{ S \subseteq \mathcal{U} }[/math] where retrieve has to return [math]\displaystyle{ b(x) }[/math] for any value [math]\displaystyle{ x \in S }[/math] and an arbitrary value from [math]\displaystyle{ \{0, 1\}^r }[/math] otherwise.

In contrast to static functions, AMQ-filters support (probabilistic) membership queries and dictionaries additionally allow operations like listing keys or looking up the value associated with a key and returning some other symbol if the key is not contained.

As can be derived from the operations, this data structure does not need to store the keys at all and may actually use less space than would be needed for a simple list of the key value pairs. This makes it attractive in situations where the associated data is small (e.g. a few bits) compared to the keys because we can save a lot by reducing the space used by keys.

To give a simple example suppose [math]\displaystyle{ n }[/math] video game names annotated with a boolean indicating whether the game contains a dog that can be petted are given. A static function built from this database can reproduce the associated flag for all names contained in the original set and an arbitrary one for other names. The size of this static function can be made to be only [math]\displaystyle{ (1 + \epsilon) n }[/math] bits for a small [math]\displaystyle{ \epsilon }[/math] which is obviously much less than any pair based representation.

Examples

A trivial example of a static function is a sorted list of the keys and values which implements all the above operations and many more. However, the retrieve on a list is slow and we implement many unneeded operations that can be removed to allow optimizations. Furthermore, we are even allowed to return junk if the queried key is not contained which we did not use at all.

Perfect hash functions

Another simple example to build a static function is using a perfect hash function: After building the PHF for our keys, store the corresponding values at the correct position for the key. As can be seen, this approach also allows updating the associated values, the keys have to be static. The correctness follows from the correctness of the perfect hash function. Using a minimum perfect hash function gives a big space improvement if the associated values are relatively small.

XOR-retrieval

Hashed filters can be categorized by their queries into OR, AND and XOR-filters. For example, the bloom filter is an AND-filter since it returns true for a membership query if all probed locations match. XOR filters work only for static retrievals and are the most promising for building them space efficiently. They are built by solving a linear system which ensures that a query for every key returns true.

Retrieval of an element

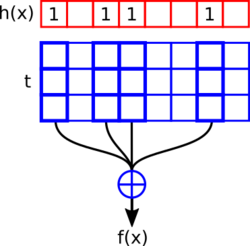
Construction

Given a hash function [math]\displaystyle{ h }[/math] that maps each key to a bitvector of length [math]\displaystyle{ m \geq \left\vert S \right\vert = n }[/math] where all [math]\displaystyle{ (h(x))_{x \in S} }[/math] are linearly independent the following system of linear equations has a solution [math]\displaystyle{ Z \in \{ 0, 1 \}^{m \times r} }[/math]:

[math]\displaystyle{ (h(x) \cdot Z = b(x))_{x \in S} }[/math]

Therefore, the static function is given by [math]\displaystyle{ h }[/math] and [math]\displaystyle{ Z }[/math] and the space usage is dominated by [math]\displaystyle{ Z }[/math] which is roughly [math]\displaystyle{ (1 + \epsilon) n }[/math] bits per key for [math]\displaystyle{ m = (1 + \epsilon) n }[/math], the hash function is assumed to be small.

A retrieval for [math]\displaystyle{ x \in \mathcal{U} }[/math] can be expressed as the bitwise XOR of the rows [math]\displaystyle{ Z_i }[/math] for all set bits [math]\displaystyle{ i }[/math] of [math]\displaystyle{ h(x) }[/math]. Furthermore, fast queries require sparse [math]\displaystyle{ h(x) }[/math], thus the problems that need to be solved for this method are finding a suitable hash function and still being able to solve the system of linear equations efficiently.

Ribbon retrieval

Using a sparse random matrix [math]\displaystyle{ h }[/math] makes retrievals cache inefficient because they access most of [math]\displaystyle{ Z }[/math] in a random non local pattern. Ribbon retrieval improves on this by giving each [math]\displaystyle{ h(x) }[/math] a consecutive "ribbon" of width [math]\displaystyle{ w = \mathcal{O}(\log n / \epsilon) }[/math] in which bits are set at random.

Using the properties of [math]\displaystyle{ (h(x))_{x \in S} }[/math] the matrix [math]\displaystyle{ Z }[/math] can be computed in [math]\displaystyle{ \mathcal{O}(n/\epsilon^2) }[/math] expected time: Ribbon solving works by first sorting the rows by their starting position (e.g. counting sort). Then, a REM form can be constructed iteratively by performing row operations on rows strictly below the current row, eliminating all 1-entries in all columns below the first 1-entry of this row. Row operations do not produce any values outside of the ribbon and are very cheap since they only require an XOR of [math]\displaystyle{ \mathcal{O}(\log n/\epsilon) }[/math] bits which can be done in [math]\displaystyle{ \mathcal{O}(1/\epsilon) }[/math] time on a RAM. It can be shown that the expected amount of row operations is [math]\displaystyle{ \mathcal{O}(n/\epsilon) }[/math]. Finally, the solution is obtained by backsubstitution.

Applications

Hash functions that lead to insertions are used to build a perfect hash function

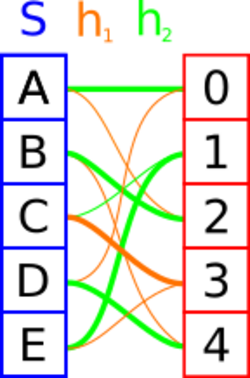
Approximate membership

To build an approximate membership data structure use a fingerprinting function [math]\displaystyle{ h \colon\, \mathcal{U} \to \{ 0, 1 \}^r }[/math]. Then build a static function [math]\displaystyle{ D_{h_S} }[/math] on [math]\displaystyle{ h_S }[/math] restricted to the domain of our keys [math]\displaystyle{ S }[/math].

Checking the membership of an element [math]\displaystyle{ x \in \mathcal{U} }[/math] is done by evaluating [math]\displaystyle{ D_{h_S} }[/math] with [math]\displaystyle{ x }[/math] and returning true if the returned value equals [math]\displaystyle{ h(x) }[/math].

• If [math]\displaystyle{ x \in S }[/math], [math]\displaystyle{ D_{h_S} }[/math]returns the correct value [math]\displaystyle{ h(x) }[/math] and we return true.
• Otherwise, [math]\displaystyle{ D_{h_S} }[/math]returns a random value and we might give a wrong answer. The length [math]\displaystyle{ r }[/math] of the hash allows controlling the false positive rate[math]\displaystyle{ f = 2^r }[/math].

The performance of this data structure is exactly the performance of the underlying static function.

Perfect hash functions

A retrieval data structure can be used to construct a perfect hash function: First insert the keys into a cuckoo hash table with [math]\displaystyle{ H=2^r }[/math] hash functions [math]\displaystyle{ h_i }[/math] and buckets of size 1. Then, for every key store the index of the hash function that lead to a key's insertion into the hash table in a [math]\displaystyle{ r }[/math]-bit retrieval data structure [math]\displaystyle{ D }[/math]. The perfect hash function is given by [math]\displaystyle{ h_{D(x)}(x) }[/math].