SP-DEVS

From HandWiki

SP-DEVS abbreviating "Schedule-Preserving Discrete Event System Specification" is a formalism for modeling and analyzing discrete event systems in both simulation and verification ways. SP-DEVS also provides modular and hierarchical modeling features which have been inherited from the Classic DEVS.

History

SP-DEVS has been designed to support verification analysis of its networks by guaranteeing to obtain a finite-vertex reachability graph of the original networks, which had been an open problem of DEVS formalism for roughly 30 years. To get such a reachability graph of its networks, SP-DEVS has been imposed the three restrictions:

  1. finiteness of event sets and state set,
  2. the lifespan of a state can be scheduled by a rational number or infinity, and
  3. preserving the internal schedule from any external events.

Thus, SP-DEVS is a sub-class of both DEVS and FD-DEVS. These three restrictions lead that SP-DEVS class is closed under coupling even though the number of states are finite. This property enables a finite-vertex graph-based verification for some qualitative properties and quantitative property, even with SP-DEVS coupled models.

Crosswalk Controller Example

System Requirements
Fig. 1. Crosswalk System
Fig. 2. SP-DEVS model for Crosswalk Light Controller

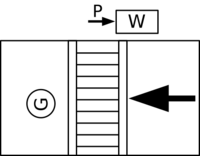
Consider a crosswalk system. Since a red light (resp. don't-walk light) behaves the opposite way of a green light (resp. walk light), for simplicity, we consider just two lights: a green light (G) and a walk light (W); and one push button as shown in Fig. 1. We want to control two lights of G and W with a set of timing constraints.

To initialize two lights, it takes 0.5 seconds to turn G on and 0.5 seconds later, W gets off. Then, every 30 seconds, there is a chance that G becomes off and W on if someone pushed the push button. For a safety reason, W becomes on two seconds after G got off. 26 seconds later, W gets off and then two seconds later G gets back on. These behaviors repeats.

Controller Design

To build a controller for above requirements, we can consider one input event 'push-button' (abbreviated by ?p) and four output events 'green-on' (!g:1), 'green-off' (!g:0), 'walk-on' (!w:1) and 'walk-off (!w:0) which will be used as commands signals for the green light and the walk light. As a set of states of the controller, we considers 'booting-green' (BG), 'booting-walk' (BW), 'green-on' (G), 'green-to-red' (GR), 'red-on' (R), 'walk-on' (W), 'delay' (D). Let's design the state transitions as shown in Fig. 2. Initially, the controller starts at BG whose lifespan is 0.5 seconds. After the lifespan, it moves to BW state at this moment, it generates the 'green-on' event, too. After 0.5 seconds staying at BW, it moves to G state whose lifespan is 30 seconds. The controller can keep staying at G by looping G to G without generating any output event or can move to GR state when it receives the external input event ?p. But, the actual staying time at GR is the remaining time for looping at G. From GR, it moves to R state with generating an output event !g:0 and its R state last two seconds then it will move to W state with output event !w:1. 26 seconds later, it moves to D state with generating !w:0 and after staying 2 seconds at D, it moves back to G with output event !g:1.

Atomic SP-DEVS

Formal Definition

The above controller for crosswalk lights can be modeled by an atomic SP-DEVS model. Formally, an atomic SP-DEVS is a 7-tuple [math]\displaystyle{ M=\lt X,Y,S,s_0, \tau, \delta_x, \delta_y\gt }[/math]

where

  • [math]\displaystyle{ X }[/math] is a finite set of input events;
  • [math]\displaystyle{ Y }[/math] is a finite set of output events;
  • [math]\displaystyle{ S }[/math] is a finite set of states;
  • [math]\displaystyle{ s_0 \in S }[/math] is the initial state;
  • [math]\displaystyle{ \tau: S \rightarrow \mathbb{Q}_{[0,\infty]} }[/math] is the time advanced function which defines the lifespan of a state where [math]\displaystyle{ \mathbb{Q}_{[0,\infty]} }[/math] is the set of non-negative rational numbers plus infinity.
  • [math]\displaystyle{ \delta_x: S \times X \rightarrow S }[/math] is the external transition function which defines how an input event changes a state of the system.
  • [math]\displaystyle{ \delta_y: S \rightarrow Y^\phi \times S }[/math] is the output and internal transition function where [math]\displaystyle{ Y^\phi = Y \cup \{\phi\} }[/math] and [math]\displaystyle{ \phi \notin Y }[/math] denotes the silent event. The output and internal transition function defines how a state generates an output event, at the same time, how the state changes internally.[1]
Formal Representation of Crosswalk Controller

The above controller shown in Fig. 2 can be written as [math]\displaystyle{ M=\lt X,Y,S,s_0, \tau, \delta_x, \delta_y\gt }[/math] where [math]\displaystyle{ X }[/math]={?p}; [math]\displaystyle{ Y }[/math]={!g:0, !g:1, !w:0, !w:1}; [math]\displaystyle{ S }[/math]={BG, BW, G, GR, R, W, D}; [math]\displaystyle{ s_0 }[/math]=BG, [math]\displaystyle{ \tau }[/math](BG)=0.5,[math]\displaystyle{ \tau }[/math](BW)=0.5, [math]\displaystyle{ \tau }[/math](G)=30, [math]\displaystyle{ \tau }[/math](GR)=30,[math]\displaystyle{ \tau }[/math](R)=2, [math]\displaystyle{ \tau }[/math](W)=26, [math]\displaystyle{ \tau }[/math](D)=2; [math]\displaystyle{ \delta_x }[/math](G,?p)=GR, [math]\displaystyle{ \delta_x }[/math](s,?p)=s if s [math]\displaystyle{ \neq }[/math]G; [math]\displaystyle{ \delta_y }[/math](BG)=(!g:1, BW), [math]\displaystyle{ \delta_y }[/math](BW)=(!w:0, G),[math]\displaystyle{ \delta_y }[/math](G)=([math]\displaystyle{ \phi }[/math], G), [math]\displaystyle{ \delta_y }[/math](GR)=(!g:0, R), [math]\displaystyle{ \delta_y }[/math](R)=(!w:1, W), [math]\displaystyle{ \delta_y }[/math](W)=(!w:0, D), [math]\displaystyle{ \delta_y }[/math](D)=(!g:1, G);

Behaviors of a SP-DEVS model

Fig. 3. Event Segment and its State Trajectory of SP-DEVS model

To captured the dynamics of an atomic SP-DEVS, we need to introduce two variables associated to time. One is the lifespan, the other is the elapsed time since the last resetting. Let [math]\displaystyle{ t_s \in \mathbb{Q}_{[0,\infty]} }[/math] be the lifespan which is not continuously increasing but set by when a discrete event happens. Let [math]\displaystyle{ t_e \in [0, \infty] }[/math] denote the elapsed time which is continuously increasing over time if there is no resetting.

Fig.3. shows a state trajectory associated with an event segment of the SP-DEVS model shown in Fig. 2. The top of Fig.3. shows an event trajectory in which the horizontal axis is a time axis so it shows an event occurs at a certain time, for example, !g:1 occurs at 0.5 and !w:0 at 1.0 time unit, and so on. The bottom of Fig. 3 shows the state trajectory associated with the above event segment in which the state [math]\displaystyle{ s \in S }[/math] is associated with its lifespan and its elapsed time in the form of [math]\displaystyle{ (s, t_s, t_e) }[/math]. For example, (G, 30, 11) denotes that the state is G, its lifespan is and the elapsed time is 11 time units. The line segments of the bottom of Fig. 3 shows the time flow of the elapsed time which is the only one continuous variable in SP-DEVS.

One interesting feature of SF-DEVS might be the preservation of schedule the restriction (3) of SP-DEVS which is drawn at time 47 in Fig. 3. when the external event ?p happens. At this moment, even though the state can change from G to GR, the elapsed time does not change so the line segment is not broken at time 47 and [math]\displaystyle{ t_e }[/math] can grow up to [math]\displaystyle{ t_e }[/math] which is 30 in this example. Due to this preservation of the schedule from input events as well as the restriction of the time advance to the non-negative rational number (see restriction (2) above), the height of every saw can be a non-negative rational number or infinity (as shown in the bottom of Fig. 3.) in a SP-DEVS model.

SP-DEVS is a sub-class of DEVS

A SP-DEVS model, [math]\displaystyle{ M=\lt X,Y,S,s_0,\tau,\delta_x, \delta_y\gt }[/math] is DEVS [math]\displaystyle{ \mathcal{M}=\lt X,Y,S',s_0',ta,\delta_{ext}, \delta_{int}, \lambda\gt }[/math] where

  • [math]\displaystyle{ X,Y }[/math] of [math]\displaystyle{ \mathcal{M} }[/math] are the same as those of [math]\displaystyle{ M }[/math].
  • [math]\displaystyle{ S'=\{(s,t_s): s \in S,t_s \in \mathbb{T}^\infty\} }[/math]
  • [math]\displaystyle{ s_0'=(s_0,\tau(s_0)) }[/math]
  • Given a state [math]\displaystyle{ (s,t_s) \in S' }[/math], [math]\displaystyle{ ta(s,t_s) = t_s. }[/math]
  • Given a state [math]\displaystyle{ (s,t_s) \in S' }[/math] and an input event [math]\displaystyle{ x \in X, \delta_{ext}(s, t_s, t_e, x) = (s',t_s - t_e) \text{ if } \delta_x(s,x)=s'. }[/math]
  • Given a state [math]\displaystyle{ (s,t_s) \in S' }[/math], [math]\displaystyle{ \delta_{int}(s,t_s)=(s',\tau(s') }[/math] if [math]\displaystyle{ \delta_{y}(s)=(y,s'). }[/math]
  • Given a state [math]\displaystyle{ (s,t_s) \in S' }[/math], [math]\displaystyle{ \lambda(s,t_s)=y }[/math] if [math]\displaystyle{ \delta_{y}(s)=(y,s'). }[/math]

Advantages

  • Applicability of Time-Line Abstraction

The property of non-negative rational-valued lifespans which are not changed by input events along with finite numbers of states and events guarantees that the behavior of SP-DEVS networks can be abstracted as an equivalent finite-vertex reachability graph by abstracting the infinitely-many values of the elapsed times.

To abstract the infinitely-many cases of elapsed times for each components of SP-DEVS networks, a time-abstraction method, called the time-line abstraction has been introduced [Hwang05],[HCZF07] in which the orders and relative difference of schedules are preserved. By using the time-line abstraction technique, the behavior of any SP-DEVS network can be abstracted as a reachability graph whose numbers of vertices and edges are finite.

  • Decidability of Safety

As a qualitative property, safety of a SP-DEVS network is decidable by (1) generating the finite-vertex reachability graph of the given network and (2) checking whether some bad states are reachable or not [Hwang05].

  • Decidability of Liveness

As a qualitative property, liveness of a SP-DEVS network is decidable by (1) generating the finite-vertex reachability graph (RG) of the given network, (2) from RG, generating kernel directed acyclic graph (KDAG) in which a vertex is strongly connected component, and (3) checking if a vertex of KDAG contains a state transition cycle which contains a set of liveness states[Hwang05].

  • Decidability of Min/Max Processing Time Bounds

As a quantitative property, minimum and maximum processing time bounds from two events in SP-DEVS networks can be computed by (1) generating the finite-vertex reachability graph and (2.a) by finding the shortest paths for the minimum processing time bound and (2.b) by finding the longest paths (if available) for the maximum processing time bound [HCZF07].

Disadvantages

  • Less Expressiveness: OPNA problem

Let a total state [math]\displaystyle{ (s,t_s,t_e) }[/math] of a SP-DEVS model be passive if [math]\displaystyle{ t_s = \infty }[/math]; otherwise, it be active.

One of known SP-DEVS's limitation is a phenomenon that "once an SP-DEVS model becomes passive, it never returns to become active (OPNA)". This phenomenon was found first at [Hwang 05b] although it was originally called ODNR ("once it dies, it never returns."). The reason why this one happens is because of the restriction (3) above in which no input event can change the schedule so the passive state can not be awaken into the active state.

For example, the toaster models drawn in Fig. 3(b) are not SP-DEVS because the total state associated with "idle" (I), is passive but it moves to an active state, "toast" (T) whose toating time is 20 seconds or 40 seconds. Actually, the model shown in Fig. 3(b) is FD-DEVS.

Tool

There is an open source library, called DEVS# at http://xsy-csharp.sourceforge.net/DEVSsharp/, that supports some algorithms for finding safeness and liveness as well as Min/Max processing time bounds.

Footnotes

  1. ↑ [math]\displaystyle{ \delta_y }[/math] can be divided into two functions: [math]\displaystyle{ \lambda: S \rightarrow Y^\phi }[/math] and [math]\displaystyle{ \delta_{int}:S \rightarrow S }[/math]as in [ZKP00].

References

  • [Hwang05] M. H. Hwang, "Tutorial: Verification of Real-time System Based on Schedule-Preserved DEVS", Proceedings of 2005 DEVS Symposium, San Diego, Apr. 2-8, 2005, ISBN:978-1-56555-293-7 (Available at http://moonho.hwang.googlepages.com/publications)
  • [Hwang05b] M. H. Hwang, "Generating Finite-State Global Behavior of Reconfigurable Automation Systems: DEVS Approach", Proceedings of 2005 IEEE-CASE, Edmonton, Canada, Aug. 1-2, 2005 (Available at http://moonho.hwang.googlepages.com/publications)
  • [HCZF07] M. H. Hwang, S.K. Cho, Bernard Zeigler, and F. Lin, "Processing Time Bounds of Schedule-Preserving DEVS", ACIMS Technical Report, 2007, (Available at http://www.acims.arizona.edu and http://moonho.hwang.googlepages.com/publications)
  • [Sedgewick02], R. Sedgewick, Algorithms in C++, Part 5 Graph Algorithm, Addison Wesley, Boston, third edition
  • [ZKP00] Bernard Zeigler, Tag Gon Kim, Herbert Praehofer (2000). Theory of Modeling and Simulation (second ed.). Academic Press, New York. ISBN 978-0-12-778455-7. 



Retrieved from "https://handwiki.org/wiki/index.php?title=SP-DEVS&oldid=2627313"