Schelling's model of segregation

Short description: Agent-based segregation model

Schelling's model of segregation is an agent-based model developed by economist Thomas Schelling. Schelling's model does not include outside factors that place pressure on agents to segregate such as Jim Crow laws in the United States, but Schelling's work does demonstrate that having people with "mild" in-group preference towards their own group could still lead to a highly segregated society via de facto segregation.

Model

Simulation of the model. Agents will move at each step until the fraction of neighbors that are from their own group is greater than or equal to [math]\displaystyle{ B_{\textrm{a}} }[/math]. For equal sized populations, [math]\displaystyle{ B_{\textrm{a}} \geq B_{\textrm{seg}}\approx 1/3 }[/math] leads to the groups segregating themselves.

The original model is set in an [math]\displaystyle{ N \times N }[/math] grid. Agents are split into two groups and occupy the spaces of the grid and only one agent can occupy a space at a time. Agents desire a fraction [math]\displaystyle{ B_{\textrm{a}} }[/math] of their neighborhood (in this case defined to be the eight adjacent agents around them) to be from the same group. Increasing [math]\displaystyle{ B_{\textrm{a}} }[/math] corresponds to increasing the agent's intolerance of outsiders.

Each round consists of agents checking their neighborhood to see if the fraction of neighbors [math]\displaystyle{ B }[/math] that matches their group—ignoring empty spaces—is greater than or equal [math]\displaystyle{ B_{\textrm{a}} }[/math]. If [math]\displaystyle{ B \lt B_{\textrm{a}} }[/math] then the agent will choose to relocate to a vacant spot where [math]\displaystyle{ B \geq B_{\textrm{a}} }[/math]. This continues until every agent is satisfied. Every agent is not guaranteed to be satisfied and in these cases it is of interest to study the patterns (if any) of the agent dynamics.

While studying populations dynamics of two groups of equal size, Schelling found a threshold [math]\displaystyle{ B_{\textrm{seg}} }[/math] such that [math]\displaystyle{ B_{\textrm{a}} \lt B_{\textrm{seg}} }[/math] leads to a random population configuration and [math]\displaystyle{ B_{\textrm{a}} \geq B_{\textrm{seg}} }[/math] leads to a segregated population. The value of [math]\displaystyle{ B_{\textrm{seg}} }[/math] was approximately [math]\displaystyle{ \frac{1}{3} }[/math]. This points to how individuals with even a small amount of in-group preference can form segregated societies. There are different parameterizations and variants of the model and a 'unified' approach is presented in allowing the simulations to explore the thresholds for different segregation events to occur.

Physical model analogies

There have been observations that the fundamental dynamics of the agents resemble the mechanics used in the Ising model of ferromagnetism. This primarily relies on the similar nature in which each occupied grid location calculates an aggregate measure based upon the similarities of the adjacent grid cells. If each agent produces a satisfaction based upon their homophilic satisfaction threshold as [math]\displaystyle{ [0,1] }[/math] then the summation of those values can provide an indication for the segregation of the state that is analogous to the clustering of the aligned spins in a magnetic material. If each cell is a member of a group [math]\displaystyle{ m_n \in {m_1,m_2,m_{empty}} }[/math], then the local homogeneity can be found via

[math]\displaystyle{ l(m_n) = \sum_{i=-1}^{1}\sum_{j=-1}^{1} \left( \delta_{m_{(ni,nj)},m_{(ni+i,nj+j)}} : i,j \neq 0 \right) }[/math] where the 1-d position of [math]\displaystyle{ n }[/math] can be translated into i,j coordinates of ni,nj. Then the state of whether the agent [math]\displaystyle{ m_n }[/math] moves to a randomly empty grid cell position or 'remains' is defined by:

Agents that have their local homogeneity constraint satisfied 'remain' [math]\displaystyle{ R }[/math] in that position between iterations. The total [math]\displaystyle{ R }[/math] for the grid is plotted as an average over 500 simulations.

[math]\displaystyle{ r\left(m_n\right) = \begin{cases} \left( l\left(m_n\right) \geq B_a \right), & \text{if} : m_n \notin { m_{empty} } \\ 0, & \text{if} : m_n \in {m_{empty}} \end{cases} }[/math]

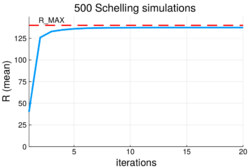
Each agent produces a binary value, so that for each grid configuration of agents of both groups, a vector can be produced of the remain due to satisfaction or not. The overall satisfaction from the remain states of all the agents can be computed;[math]\displaystyle{ R = \sum_{n=1}^{N}r(m_n) }[/math].

[math]\displaystyle{ R }[/math] then provides a measure for the amount of homogeneity (segregation) on the grid and can be used with the maximum possible value (total sum of agents) as a 'density' of segregation over the simulation of movements as is performed in. Following the approach of [math]\displaystyle{ R }[/math] can be interpreted as a macrostate whose density [math]\displaystyle{ \Omega }[/math] can be estimated by sampling via the Monte Carlo method the grid space from the random initialisations of the grid to produce a calculation of the entropy; [math]\displaystyle{ S = k_B \text{ln} \Omega(R). }[/math] This allows a trace of the entropy to be computed over the iterations of the simulation as is done with other physical systems.

Broader model considerations

The canonical Schelling model does not consider variables which may affect the agent's ability to relocate positions in the grid. The work of investigates a model extension where the utility available to agents to move governs this action. It can explain some of the patterns seen where groups do not segregate due to the financial barrier homogeneous zones produce as a result of high demand. The consideration of the financial aspect is also investigated in and. The work of further develops this concept of the importance of the monetary factor in the decision making, and uses it to extend the model with a dual dynamic where agents radiate their income store whenever a movement is made. This also provides a means to produce a more complete model where the trace of the entropy is non-decreasing and adds support that social systems obey the Second law of thermodynamics.

Schelling's model has also been studied from a game-theoretic perspective: In Schelling games, agents strategically strive to maximize their utilities by relocating to a position with the highest fraction of neighboring agents from the same group.

See also

• Critical mass
• Domino effect
• Gerrymandering
• Social dynamics
• Tipping point