Schinzel's theorem
In the geometry of numbers, Schinzel's theorem is the following statement:
Schinzel's theorem — For any given positive integer [math]\displaystyle{ n }[/math], there exists a circle in the Euclidean plane that passes through exactly [math]\displaystyle{ n }[/math] integer points.
It was originally proved by and named after Andrzej Schinzel.[1][2]
Proof
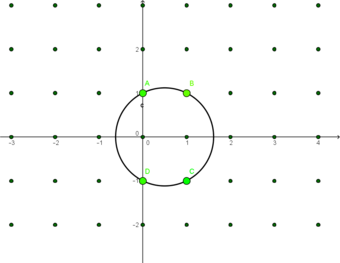
Schinzel proved this theorem by the following construction. If [math]\displaystyle{ n }[/math] is an even number, with [math]\displaystyle{ n=2k }[/math], then the circle given by the following equation passes through exactly [math]\displaystyle{ n }[/math] points:[1][2] [math]\displaystyle{ \left(x-\frac{1}{2}\right)^2 + y^2 = \frac{1}{4} 5^{k-1}. }[/math] This circle has radius [math]\displaystyle{ 5^{(k-1)/2}/2 }[/math], and is centered at the point [math]\displaystyle{ (\tfrac12,0) }[/math]. For instance, the figure shows a circle with radius [math]\displaystyle{ \sqrt 5/2 }[/math] through four integer points.
Multiplying both sides of Schinzel's equation by four produces an equivalent equation in integers, [math]\displaystyle{ \left(2x-1\right)^2 + (2y)^2 = 5^{k-1}. }[/math] This writes [math]\displaystyle{ 5^{k-1} }[/math] as a sum of two squares, where the first is odd and the second is even. There are exactly [math]\displaystyle{ 4k }[/math] ways to write [math]\displaystyle{ 5^{k-1} }[/math] as a sum of two squares, and half are in the order (odd, even) by symmetry. For example, [math]\displaystyle{ 5^1=(\pm 1)^2 + (\pm 2)^2 }[/math], so we have [math]\displaystyle{ 2x-1=1 }[/math] or [math]\displaystyle{ 2x-1=-1 }[/math], and [math]\displaystyle{ 2y=2 }[/math] or [math]\displaystyle{ 2y=-2 }[/math], which produces the four points pictured.
On the other hand, if [math]\displaystyle{ n }[/math] is odd, with [math]\displaystyle{ n=2k+1 }[/math], then the circle given by the following equation passes through exactly [math]\displaystyle{ n }[/math] points:[1][2] [math]\displaystyle{ \left(x-\frac{1}{3}\right)^2 + y^2 = \frac{1}{9} 5^{2k}. }[/math] This circle has radius [math]\displaystyle{ 5^k/3 }[/math], and is centered at the point [math]\displaystyle{ (\tfrac13,0) }[/math].
Properties
The circles generated by Schinzel's construction are not the smallest possible circles passing through the given number of integer points,[3] but they have the advantage that they are described by an explicit equation.[2]
References
- ↑ 1.0 1.1 1.2 "Sur l'existence d'un cercle passant par un nombre donné de points aux coordonnées entières" (in fr), L'Enseignement mathématique 4: 71–72, 1958
- ↑ 2.0 2.1 2.2 2.3 "Schinzel's theorem", Mathematical Gems I, Dolciani Mathematical Expositions, 1, Mathematical Association of America, 1973, pp. 118–121
- ↑ Weisstein, Eric W.. "Schinzel Circle". http://mathworld.wolfram.com/SchinzelCircle.html.
 |