Scorer's function

Graph of [math]\displaystyle{ \mathrm{Gi}(x) }[/math] and [math]\displaystyle{ \mathrm{Hi}(x) }[/math]

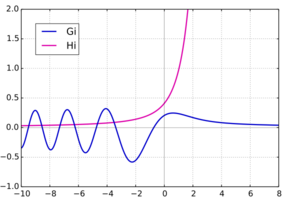
In mathematics, the Scorer's functions are special functions studied by (Scorer 1950) and denoted Gi(x) and Hi(x).

Hi(x) and -Gi(x) solve the equation

[math]\displaystyle{ y''(x) - x\ y(x) = \frac{1}{\pi} }[/math]

and are given by

[math]\displaystyle{ \mathrm{Gi}(x) = \frac{1}{\pi} \int_0^\infty \sin\left(\frac{t^3}{3} + xt\right)\, dt, }[/math]

[math]\displaystyle{ \mathrm{Hi}(x) = \frac{1}{\pi} \int_0^\infty \exp\left(-\frac{t^3}{3} + xt\right)\, dt. }[/math]

The Scorer's functions can also be defined in terms of Airy functions:

[math]\displaystyle{ \begin{align} \mathrm{Gi}(x) &{}= \mathrm{Bi}(x) \int_x^\infty \mathrm{Ai}(t) \, dt + \mathrm{Ai}(x) \int_0^x \mathrm{Bi}(t) \, dt, \\ \mathrm{Hi}(x) &{}= \mathrm{Bi}(x) \int_{-\infty}^x \mathrm{Ai}(t) \, dt - \mathrm{Ai}(x) \int_{-\infty}^x \mathrm{Bi}(t) \, dt. \end{align} }[/math]

• 

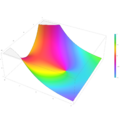
  Plot of the Scorer function Gi(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D

• 

  Plot of the derivative of the Scorer function Hi'(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D

• 

  Plot of the derivative of the Scorer function Gi'(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D

• Error creating thumbnail: Unable to save thumbnail to destination

  Plot of the Scorer function Hi(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D

References

• Olver, F. W. J. (2010), "Scorer functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, http://dlmf.nist.gov/9.12 
• Scorer, R. S. (1950), "Numerical evaluation of integrals of the form [math]\displaystyle{ I=\int^{x_2}_{x_{1}}f(x)e^{i\phi(x)}dx }[/math] and the tabulation of the function [math]\displaystyle{ {\rm Gi} (z)=\frac{1}{\pi}\int^\infty_0{\rm sin}\left(uz+\frac 13 u^3\right)du }[/math]", The Quarterly Journal of Mechanics and Applied Mathematics 3: 107–112, doi:10.1093/qjmam/3.1.107, ISSN 0033-5614