Semi-invariant of a quiver

In mathematics, given a quiver Q with set of vertices Q₀ and set of arrows Q₁, a representation of Q assigns a vector space V_i to each vertex and a linear map V(α): V(s(α)) → V(t(α)) to each arrow α, where s(α), t(α) are, respectively, the starting and the ending vertices of α. Given an element d ∈ [math]\displaystyle{ \mathbb{N} }[/math]^Q₀, the set of representations of Q with dim V_i = d(i) for each i has a vector space structure.

It is naturally endowed with an action of the algebraic group Π_i∈Q0 GL(d(i)) by simultaneous base change. Such action induces one on the ring of functions. The ones which are invariants up to a character of the group are called semi-invariants. They form a ring whose structure reflects representation-theoretical properties of the quiver.

Definitions

Let Q = (Q₀,Q₁,s,t) be a quiver. Consider a dimension vector d, that is an element in [math]\displaystyle{ \mathbb{N} }[/math]^Q₀. The set of d-dimensional representations is given by

[math]\displaystyle{ \operatorname{Rep}(Q,\mathbf{d}):=\{V\in \operatorname{Rep}(Q) : V_i = \mathbf{d}(i)\} }[/math]

Once fixed bases for each vector space V_i this can be identified with the vector space

[math]\displaystyle{ \bigoplus_{\alpha\in Q_1} \operatorname{Hom}_k(k^{\mathbf{d}(s(\alpha))}, k^{\mathbf{d}(t(\alpha))}) }[/math]

Such affine variety is endowed with an action of the algebraic group GL(d) := Π_{i∈ Q0} GL(d(i)) by simultaneous base change on each vertex:

[math]\displaystyle{ \begin{array}{ccc} GL(\mathbf{d}) \times \operatorname{Rep}(Q,\mathbf{d}) & \longrightarrow & \operatorname{Rep}(Q,\mathbf{d})\\ \Big((g_i), (V_i, V(\alpha))\Big) & \longmapsto & (V_i,g_{t(\alpha)}\cdot V(\alpha)\cdot g_{s(\alpha)}^{-1} ) \end{array} }[/math]

By definition two modules M,N ∈ Rep(Q,d) are isomorphic if and only if their GL(d)-orbits coincide.

We have an induced action on the coordinate ring k[Rep(Q,d)] by defining:

[math]\displaystyle{ \begin{array}{ccc} GL(\mathbf{d}) \times k[\operatorname{Rep}(Q,\mathbf{d})] & \longrightarrow & k[\operatorname{Rep}(Q,\mathbf{d})]\\ (g, f) & \longmapsto & g\cdot f(-):=f(g^{-1}. -) \end{array} }[/math]

Polynomial invariants

An element f ∈ k[Rep(Q,d)] is called an invariant (with respect to GL(d)) if g⋅f = f for any g ∈ GL(d). The set of invariants

[math]\displaystyle{ I(Q,\mathbf{d}):=k[\operatorname{Rep}(Q,\mathbf{d})]^{GL(\mathbf{d})} }[/math]

is in general a subalgebra of k[Rep(Q,d)].

Example

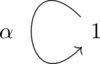
Consider the 1-loop quiver Q:

For d = (n) the representation space is End(kⁿ) and the action of GL(n) is given by usual conjugation. The invariant ring is

[math]\displaystyle{ I(Q,\mathbf{d})=k[c_1,\ldots,c_n] }[/math]

where the c_is are defined, for any A ∈ End(kⁿ), as the coefficients of the characteristic polynomial

[math]\displaystyle{ \det(A-t \mathbb{I})=t^n-c_1(A)t^{n-1}+\cdots+(-1)^n c_n(A) }[/math]

Semi-invariants

In case Q has neither loops nor cycles the variety k[Rep(Q,d)] has a unique closed orbit corresponding to the unique d-dimensional semi-simple representation, therefore any invariant function is constant.

Elements which are invariants with respect to the subgroup SL(d) := Π_{{i ∈ Q0}} SL(d(i)) form a ring, SI(Q,d), with a richer structure called ring of semi-invariants. It decomposes as

[math]\displaystyle{ SI(Q,\mathbf{d})=\bigoplus_{\sigma\in \mathbb{Z}^{Q_0}} SI(Q,\mathbf{d})_{\sigma} }[/math]

where

[math]\displaystyle{ SI(Q,\mathbf{d})_{\sigma}:= \{f\in k[\operatorname{Rep}(Q,\mathbf{d})] : g\cdot f = \prod_{i\in Q_0}\det(g_i)^{\sigma_i} f, \forall g\in GL(\mathbf{d})\}. }[/math]

A function belonging to SI(Q,d)_σ is called semi-invariant of weight σ.

Example

Consider the quiver Q:

[math]\displaystyle{ 1 \xrightarrow{\ \ \alpha\ } 2 }[/math]

Fix d = (n,n). In this case k[Rep(Q,(n,n))] is congruent to the set of square matrices of size n: M(n). The function defined, for any B ∈ M(n), as det^u(B(α)) is a semi-invariant of weight (u,−u) in fact

[math]\displaystyle{ (g_1,g_2)\cdot {\det}^u (B) = {\det}^u(g_2^{-1}B g_1)= {\det}^u(g_1) {\det}^{-u}(g_2) {\det}^u(B) }[/math]

The ring of semi-invariants equals the polynomial ring generated by det, i.e.

[math]\displaystyle{ \mathsf{SI}(Q,\mathbf{d})=k[\det] }[/math]

Characterization of representation type through semi-invariant theory

For quivers of finite representation-type, that is to say Dynkin quivers, the vector space k[Rep(Q,d)] admits an open dense orbit. In other words, it is a prehomogenous vector space. Sato and Kimura described the ring of semi-invariants in such case.

Sato–Kimura theorem

Let Q be a Dynkin quiver, d a dimension vector. Let Σ be the set of weights σ such that there exists f_σ ∈ SI(Q,d)_σ non-zero and irreducible. Then the following properties hold true.

i) For every weight σ we have dim_k SI(Q,d)_σ ≤ 1.

ii) All weights in Σ are linearly independent over [math]\displaystyle{ \mathbb{Q} }[/math].

iii) SI(Q,d) is the polynomial ring generated by the f_σ's, σ ∈ Σ.

Furthermore, we have an interpretation for the generators of this polynomial algebra. Let O be the open orbit, then k[Rep(Q,d)] \ O = Z₁ ∪ ... ∪ Z_t where each Z_i is closed and irreducible. We can assume that the Z_is are arranged in increasing order with respect to the codimension so that the first l have codimension one and Z_i is the zero-set of the irreducible polynomial f₁, then SI(Q,d) = k[f₁, ..., f_l].

Example

In the example above the action of GL(n,n) has an open orbit on M(n) consisting of invertible matrices. Then we immediately recover SI(Q,(n,n)) = k[det].

Skowronski–Weyman provided a geometric characterization of the class of tame quivers (i.e. Dynkin and Euclidean quivers) in terms of semi-invariants.

Skowronski–Weyman theorem

Let Q be a finite connected quiver. The following are equivalent:

i) Q is either a Dynkin quiver or a Euclidean quiver.

ii) For each dimension vector d, the algebra SI(Q,d) is complete intersection.

iii) For each dimension vector d, the algebra SI(Q,d) is either a polynomial algebra or a hypersurface.

Example

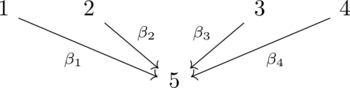
Consider the Euclidean quiver Q:

Pick the dimension vector d = (1,1,1,1,2). An element V ∈ k[Rep(Q,d)] can be identified with a 4-ple (A₁, A₂, A₃, A₄) of matrices in M(1,2). Call D_i,j the function defined on each V as det(A_i,A_j). Such functions generate the ring of semi-invariants:

[math]\displaystyle{ SI(Q,\mathbf{d})=\frac{k[D_{1,2},D_{3,4},D_{1,4},D_{2,3},D_{1,3},D_{2,4}]}{D_{1,2}D_{3,4}+D_{1,4}D_{2,3}-D_{1,3}D_{2,4}} }[/math]

See also

• Wild problem

References

• Derksen, H.; Weyman, J. (2000), "Semi-invariants of quivers and saturation for Littlewood–Richardson coefficients.", J. Amer. Math. Soc. 3 (13): 467–479, doi:10.1090/S0894-0347-00-00331-3, http://www.ams.org/journals/jams/2000-13-03/S0894-0347-00-00331-3/home.html 
• Sato, M.; Kimura, T. (1977), "A classification of irreducible prehomogeneous vector spaces and their relative invariants.", Nagoya Math. J. 65: 1–155, doi:10.1017/S0027763000017633, http://projecteuclid.org/euclid.nmj/1118796150 
• Skowronski, A.; Weyman, J. (2000), "The algebras of semi-invariants of quivers.", Transform. Groups 5 (4): 361–402, doi:10.1007/bf01234798