Shallow minor

Short description: Graph minor formed from subgraphs of small diameter

In graph theory, a shallow minor or limited-depth minor is a restricted form of a graph minor in which the subgraphs that are contracted to form the minor have small diameter. Shallow minors were introduced by (Plotkin Rao), who attributed their invention to Charles E. Leiserson and Sivan Toledo.

Definition

A graph that has the complete graph K₄ as a 1-shallow minor. Each of the four vertex subsets indicated by the dashed rectangles induces a connected subgraph with radius one, and there exists an edge between every pair of subsets.

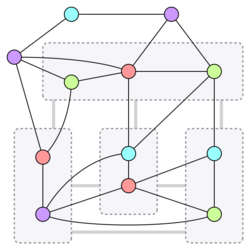
One way of defining a minor of an undirected graph G is by specifying a subgraph H of G, and a collection of disjoint subsets S_i of the vertices of G, each of which forms a connected induced subgraph H_i of H. The minor has a vertex v_i for each subset S_i, and an edge v_iv_j whenever there exists an edge from S_i to S_j that belongs to H.

In this formulation, a d-shallow minor (alternatively called a shallow minor of depth d) is a minor that can be defined in such a way that each of the subgraphs H_i has radius at most d, meaning that it contains a central vertex c_i that is within distance d of all the other vertices of H_i. Note that this distance is measured by hop count in H_i, and because of that it may be larger than the distance in G.

Special cases

Shallow minors of depth zero are the same thing as subgraphs of the given graph. For sufficiently large values of d (including all values at least as large as the number of vertices), the d-shallow minors of a given graph coincide with all of its minors.

Classification of graph families

(Nešetřil Ossona de Mendez) use shallow minors to partition the families of finite graphs into two types. They say that a graph family F is somewhere dense if there exists a finite value of d for which the d-shallow minors of graphs in F consist of every finite graph. Otherwise, they say that a graph family is nowhere dense. This terminology is justified by the fact that, if F is a nowhere dense class of graphs, then (for every ε > 0) the n-vertex graphs in F have O(n^1 + ε) edges; thus, the nowhere dense graphs are sparse graphs.

A more restrictive type of graph family, described similarly, are the graph families of bounded expansion. These are graph families for which there exists a function f such that the ratio of edges to vertices in every d-shallow minor is at most f(d). If this function exists and is bounded by a polynomial, the graph family is said to have polynomial expansion.

Separator theorems

As (Plotkin Rao) showed, graphs with excluded shallow minors can be partitioned analogously to the planar separator theorem for planar graphs. In particular, if the complete graph K_h is not a d-shallow minor of an n-vertex graph G, then there exists a subset S of G, with size O(dh² log n + n/d), such that each connected component of G\S has at most 2n/3 vertices. The result is constructive: there exists a polynomial time algorithm that either finds such a separator, or a d-shallow K_h minor. As a consequence they showed that every minor-closed graph family obeys a separator theorem almost as strong as the one for planar graphs.

Plotkin et al. also applied this result to the partitioning of finite element method meshes in higher dimensions; for this generalization, shallow minors are necessary, as (with no depth restriction) the family of meshes in three or more dimensions has all graphs as minors. (Teng 1998) extends these results to a broader class of high-dimensional graphs.

More generally, a hereditary graph family has a separator theorem where the separator size is a sublinear power of n if and only if it has polynomial expansion.

References

• Strongly sublinear separators and polynomial expansion, 2015, Bibcode: 2015arXiv150404821D .
• Plotkin, Serge; Rao, Satish; Smith, Warren D. (1994), "Shallow excluded minors and improved graph decompositions", Proc. 5th ACM-SIAM Symp. on Discrete Algorithms (SODA), pp. 462–470, http://www.stanford.edu/~plotkin/lminors.ps .
• "Combinatorial aspects of geometric graphs", Comput. Geom. 9 (4): 277–287, 1998, doi:10.1016/S0925-7721(96)00008-9 .
• Wulff-Nilsen, Christian (2011), "Separator Theorems for Minor-Free and Shallow Minor-Free Graphs with Applications", Proc. 52nd IEEE Symp. Foundations of Computer Science (FOCS), pp. 37–46, doi:10.1109/FOCS.2011.15 .
• Sparsity: Graphs, Structures, and Algorithms, Algorithms and Combinatorics, 28, Springer, 2012, doi:10.1007/978-3-642-27875-4, ISBN 978-3-642-27874-7 .