Small-gain theorem

Short description: Theorem used for studying closed-loop stability

Feedback connection between systems S₁ and S₂.

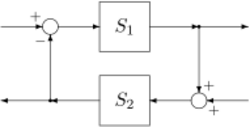
In nonlinear systems, the formalism of input-output stability is an important tool in studying the stability of interconnected systems since the gain of a system directly relates to how the norm of a signal increases or decreases as it passes through the system. The small-gain theorem gives a sufficient condition for finite-gain [math]\displaystyle{ \mathcal{L} }[/math] stability of the feedback connection. The small gain theorem was proved by George Zames in 1966. It can be seen as a generalization of the Nyquist criterion to non-linear time-varying MIMO systems (systems with multiple inputs and multiple outputs).

Theorem. Assume two stable systems [math]\displaystyle{ S_1 }[/math] and [math]\displaystyle{ S_2 }[/math] are connected in a feedback loop, then the closed loop system is input-output stable if [math]\displaystyle{ \|S_1\| \cdot \|S_2\| \lt 1 }[/math] and both [math]\displaystyle{ S_1 }[/math] and [math]\displaystyle{ S_2 }[/math] are stable by themselves. (This norm is typically the [math]\displaystyle{ \mathcal{H} \infty }[/math]-norm, the size of the largest singular value of the transfer function over all frequencies. Any induced Norm will also lead to the same results).

References

• H. K. Khalil, Nonlinear Systems, third edition, Prentice Hall, Upper Saddle River, New Jersey, 2002;
• C. A. Desoer, M. Vidyasagar, Feedback Systems: Input-Output Properties, second edition, SIAM, 2009.

See also

• Input-to-state stability