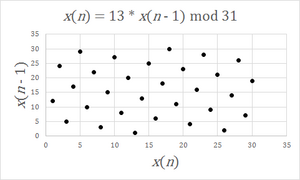
Spectral test

Three-dimensional plot of 100,000 values generated with RANDU. Each point represents 3 consecutive pseudorandom values. It is clearly seen that the points fall in 15 two-dimensional planes.

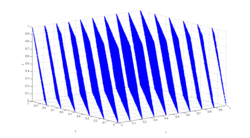
The spectral test is a statistical test for the quality of a class of pseudorandom number generators (PRNGs), the linear congruential generators (LCGs). LCGs have a property that when plotted in 2 or more dimensions, lines or hyperplanes will form, on which all possible outputs can be found. The spectral test compares the distance between these planes; the further apart they are, the worse the generator is. As this test is devised to study the lattice structures of LCGs, it can not be applied to other families of PRNGs.

According to Donald Knuth, this is by far the most powerful test known, because it can fail LCGs which pass most statistical tests. The IBM subroutine RANDU LCG fails in this test for 3 dimensions and above.

Let the PRNG generate a sequence [math]\displaystyle{ u_1, u_2, \dots }[/math]. Let [math]\displaystyle{ 1/\nu_t }[/math] be the maximal separation between covering parallel planes of the sequence [math]\displaystyle{ \{(u_{n+1:n+t}) | n = 0, 1, \dots\} }[/math]. The spectral test checks that the sequence [math]\displaystyle{ \nu_2, \nu_3, \nu_4, \dots }[/math] does not decay too quickly.

Knuth recommends checking that each of the following 5 numbers is larger than 0.01.[math]\displaystyle{ \begin{aligned} \mu_2 &= \pi \nu_2^2 / m, & \mu_3 &= \frac{4}{3} \pi \nu_3^3 / m, & \mu_4 &= \frac{1}{2} \pi^2 \nu_4^4 / m \\[1ex] && \mu_5 &= \frac{8}{15} \pi^2 \nu_5^5 / m, & \mu_6 &= \frac{1}{6} \pi^3 \nu_6^6 / m \end{aligned} }[/math]where [math]\displaystyle{ m }[/math] is the modulus of the LCG.

Examples

Examples from , especially Table 1 and discussions following it.

A small variant of the infamous RANDU, with [math]\displaystyle{ x_{n+1} = 65539 x_n \bmod 2^{29} }[/math] has [math]\displaystyle{ \mu_i = 3.14, 10^{-5}, 10^{-4}, 10^{-3}, 0.02 }[/math][math]\displaystyle{ \nu^2_i = 536936458, 118, 116, 116, 116 }[/math]

where [math]\displaystyle{ i = 2, 3, 4, 5, 6 }[/math].

George Marsaglia considers [math]\displaystyle{ x_{n+1} = 69069 x_n \bmod 2^{32} }[/math] as "a candidate for the best of all multipliers" because it is easy to remember, and has particularly large spectral test numbers:

[math]\displaystyle{ \nu^2_i = 4243209856, 2072544, 52804, 6990, 242 }[/math]

Despite the fact that both relations pass the Chi-squared test, the first LCG is less random than the second, as the range of values it can produce by the order it produces them in is less evenly distributed.