Spider diagram
In mathematics, a unitary spider diagram adds existential points to an Euler or a Venn diagram. The points indicate the existence of an attribute described by the intersection of contours in the Euler diagram. These points may be joined forming a shape like a spider. Joined points represent an "or" condition, also known as a logical disjunction.
A spider diagram is a boolean expression involving unitary spider diagrams and the logical symbols [math]\displaystyle{ \land,\lor,\lnot }[/math]. For example, it may consist of the conjunction of two spider diagrams, the disjunction of two spider diagrams, or the negation of a spider diagram.
Example
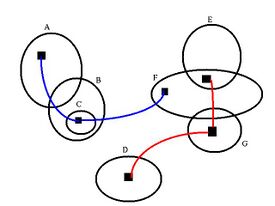
In the image shown, the following conjunctions are apparent from the Euler diagram.
- [math]\displaystyle{ A \land B }[/math]
- [math]\displaystyle{ B \land C }[/math]
- [math]\displaystyle{ F \land E }[/math]
- [math]\displaystyle{ G \land F }[/math]
In the universe of discourse defined by this Euler diagram, in addition to the conjunctions specified above, all of the sets from A through G, except for C, are available separately. The set C is only available as a subset of B. Often, in complicated diagrams, singleton sets and/or conjunctions may be obscured by other set combinations.
The two spiders in the example correspond to the following logical expressions:
- Red spider: [math]\displaystyle{ (F \land E) \lor (G) \lor (D) }[/math]
- Blue spider: [math]\displaystyle{ (A) \lor (C \land B) \lor (F) }[/math]
References
- Howse, J. and Stapleton, G. and Taylor, H. Spider Diagrams London Mathematical Society Journal of Computation and Mathematics, (2005) v. 8, pp. 145–194. ISSN 1461-1570 Accessed on January 8, 2012 here
- Stapleton, G. and Howse, J. and Taylor, J. and Thompson, S. What can spider diagrams say? Proc. Diagrams, (2004) v. 168, pp. 169–219. Accessed on January 4, 2012 here
- Stapleton, G. and Jamnik, M. and Masthoff, J. On the Readability of Diagrammatic Proofs Proc. Automated Reasoning Workshop, 2009. PDF
External links
 |  |
