Stokes phenomenon

In complex analysis the Stokes phenomenon, discovered by G. G. Stokes (1847, 1858), is where the asymptotic behavior of functions can differ in different regions of the complex plane. This seemingly gives rise to a paradox when looking at the asymptotic expansion of an analytic function. Since an analytic function is continuous you would expect the asymptotic expansion to be continuous. This paradox is the subject of Stokes' early research and is known as Stokes phenomenon. The regions in the complex plane with different asymptotic behaviour are bounded by possibly one or two types of curves known as Stokes curves and Anti-Stokes Curves. This apparent paradox has since been resolved and the supposed discontinuous jump in the asymptotic expansions has been shown to be smooth and continuous. In order to resolve this paradox the asymptotic expansion needs to be handled in a careful manner. More specifically the asymptotic expansion must include additional exponentially small terms relative to the usual algebraic terms included in a usual asymptotic expansion. What happens in Stokes phenomenon is that an asymptotic expansion in one region may contain an exponentially small contribution (neglecting this contribution still gives a correct asymptotic expansion for that region). However, this exponentially small term can become exponentially large in another region of the complex plane, this change occurs across the Anti-Stokes curves. Furthermore the exponentially small term may switch on or off other exponentially small terms, this change occurs across a Stokes curve. Including these exponentially small terms allows the asymptotic expansion to be written as a continuous expansion for the entire complex domain which resolves the Stokes Phenomenon paradox.

Stokes Curves and anti-Stokes Curves

Across a Stokes curve, an exponentially small term can switch on or off another exponentially small term.

Across an anti-Stokes curve, a subdominant exponentially small term can switch to a dominant exponentially large term or vice versa.

This change in behaviour across the Stokes and anti-Stokes curves is directly related to the divergence of the asymptotic expansion. The usual type of divergence seen in an asymptotic series that exhibits Stokes phenomenon is known as factorial-over-power divergence and has the typical form

[math]\displaystyle{ \sum_j^\infty \epsilon^j \frac{A\Gamma(j+\alpha)}{\chi^{j+\alpha}}, }[/math]

Where [math]\displaystyle{ A }[/math] is a function known as the prefactor, [math]\displaystyle{ \chi }[/math] is a function known as the Singulant and [math]\displaystyle{ \Gamma }[/math] is the gamma function.

Stokes curves are determined using the condition [math]\displaystyle{ \Im\{\chi\}=0 }[/math] and [math]\displaystyle{ \Re\{\chi\}\gt 0 }[/math]. Anti Stokes curve are determined by the condition [math]\displaystyle{ \Re\{\chi\}=0 }[/math].

Example: the Airy function

The Airy function Ai(x) is one of two solutions to a simple differential equation

[math]\displaystyle{ y'' - xy = 0 , \, }[/math]

which it is often useful to approximate for many values of x – including complex values. For large x of given argument the solution can be approximated by a linear combination of the functions

[math]\displaystyle{ \frac{e^{\pm\frac23x^{3/2}}}{x^{1/4}}. }[/math]

However, the linear combination has to change as the argument of x passes certain values (when x crosses a branch cut) because these approximations contain multi-valued functions. In contrast, the Airy function is single valued and indeed entire and therefore, in order to make sense of the approximation, one has to choose a single value out of the multiple possible values (this imposes a branch cut for the approximation, by implication). For example, if we regard the limit of x as large and real, and would like to approximate the Airy function for both positive and negative values, we would find that

Plot of Ai(x) in red and Bi(x) in blue

[math]\displaystyle{ \begin{align} \mathrm{Ai}(x) &{}\sim \frac{e^{-\frac23x^{3/2}}}{2\sqrt\pi\,x^{1/4}} \\ \mathrm{Ai}(-x) &{}\sim \frac{\sin(\frac23x^{3/2}+\frac14\pi)}{\sqrt\pi\,x^{1/4}} \\ \end{align} }[/math]

Stokes lines and anti-Stokes lines for the Airy function

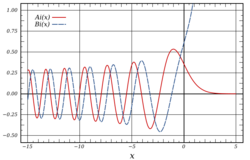
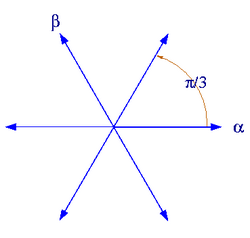
which are two very different expressions. What has happened is that as we have increased the argument of x from 0 to pi (rotating it around through the upper half complex plane) we have crossed an anti-Stokes line, which in this case is at [math]\displaystyle{ \operatorname{arg}\, x = \pi / 3 }[/math]. At this anti-Stokes line, the coefficient of [math]\displaystyle{ \frac{e^{-\frac23x^{3/2}}}{x^{1/4}} }[/math] is forced to jump. The coefficient of [math]\displaystyle{ \frac{e^{+\frac23x^{3/2}}}{x^{1/4}} }[/math] can jump at this line but is not forced to; it can change gradually as arg x varies from π/3 to π because it is not determined in this region.

There are three anti-Stokes lines with arguments π/3, π. –π/3, and three Stokes lines with arguments 2π/3, 0. –2π/3.

Example: second order linear differential equations

The Airy function example can be generalized to a broad class of second order linear differential equations as follows. By standard changes of variables, a second order equation can often be changed to one of the form

[math]\displaystyle{ \frac{d^2w}{dz^2} = f(z)w }[/math]

where f is holomorphic in a simply-connected region and w is a solution of the differential equation. Then in some cases the WKB method gives an asymptotic approximation for w as a linear combination of functions of the form

[math]\displaystyle{ \frac{e^{\pm\int_a^z\sqrt{f(z')} \, dz'}}{f(z)^{1/4}} }[/math]

for some constant a. (Choosing different values of a is equivalent to choosing different coefficients in the linear combination.) The anti-Stokes lines and Stokes lines are then the zeros of the real and imaginary parts, respectively, of

[math]\displaystyle{ \int_a^z\sqrt{f(z')} \, dz'. }[/math]

If a is a simple zero of f then locally f looks like [math]\displaystyle{ f'(a)(z-a) }[/math]. Solutions will locally behave like the Airy functions; they will have three Stokes lines and three anti-Stokes lines meeting at a.

See also

• Borel summation

References

• Berry, M. V. (1988), "Stokes' phenomenon; smoothing a Victorian discontinuity.", Inst. Hautes Études Sci. Publ. Math. 68: 211–221, doi:10.1007/bf02698550, http://www.numdam.org/item?id=PMIHES_1988__68__211_0 
• Berry, M. V. (1989), "Uniform asymptotic smoothing of Stokes's discontinuities", Proc. R. Soc. Lond. A 422 (1862): 7–21, doi:10.1098/rspa.1989.0018, Bibcode: 1989RSPSA.422....7B 
• Meyer, R. E. (1989), "A simple explanation of the Stokes phenomenon", SIAM Rev. 31 (3): 435–445, doi:10.1137/1031090, http://www.dtic.mil/get-tr-doc/pdf?AD=ADA193253 
• Olver, Frank William John (1997), Asymptotics and special functions, AKP Classics, Wellesley, MA: A K Peters Ltd., ISBN 978-1-56881-069-0 
• Stokes, G. G. (1847), "On the numerical calculation of a class of definite integrals and infinite series", Transactions of the Cambridge Philosophical Society IX (I): 166–189, https://archive.org/details/transactionsofca09camb 
• Stokes, G. G. (1858), "On the discontinuity of arbitrary constants which appear in divergent developments", Transactions of the Cambridge Philosophical Society X (I): 105–128, https://archive.org/details/transactionsofca10camb 
• Witten, Ed (2010). "Analytic Continuation Of Chern-Simons Theory". arXiv:1001.2933v4 [hep-th].
• Bender, Carl M.; Orszag, Steven A. (1978), Advanced Mathematical Methods for Scientists and Engineers, International series in pure and applied mathematics, McGraw Hill Inc., ISBN 0-07-004452-X 
• Ablowitz, M. J., & Fokas, A. S. (2003). Complex variables: introduction and applications. Cambridge University Press .