Stress–strength analysis
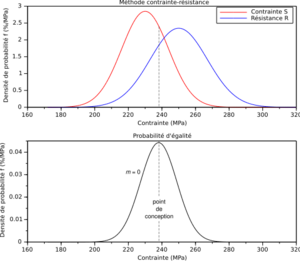

Stress–strength analysis is the analysis of the strength of the materials and the interference of the stresses placed on the materials, where "materials" is not necessarily the raw goods or parts, but can be an entire system. Stress-Strength Analysis is a tool used in reliability engineering.
Environmental stresses have a distribution with a mean and a standard deviation and component strengths have a distribution with a mean and a standard deviation . The overlap of these distributions is the probability of failure . This overlap is also referred to stress-strength interference.
Reliability
If the distributions for both the stress and the strength both follow a Normal distribution, then the reliability (R) of a component can be determined by the following equation:[1] , where
P(Z) can be determined from a Z table or a statistical software package.
See also
References
- ↑ Tersmette, Trevor. "Mechanical Stress/Strength Interference Theory". http://www.theriac.org/DeskReference/PDFs/4Q2003.pdf. Retrieved 26 February 2013.
- http://reliawiki.org/index.php/Stress-Strength_Analysis
- http://www.engr.iupui.edu/me/courses/stressstrengthinterference.pdf
 |
