Structural holes

Short description: Gap between two individuals who have complementary sources to information

Structural holes is a concept from social network research, originally developed by Ronald Stuart Burt. A structural hole is understood as a gap between two individuals who have complementary sources to information. The study of structural holes spans the fields of sociology, economics, and computer science. Burt introduced this concept in an attempt to explain the origin of differences in social capital. Burt’s theory suggests that individuals hold certain positional advantages/disadvantages from how they are embedded in neighborhoods or other social structures.

The concept

Most social structures tend to be characterized by dense clusters of strong connections, also known as network closure. The theory relies on a fundamental idea that the homogeneity of information, new ideas, and behavior is generally higher within any group of people as compared to that in between two groups of people. An individual who acts as a mediator between two or more closely connected groups of people could gain important comparative advantages. In particular, the position of a bridge between distinct groups allows him or her to transfer or gatekeep valuable information from one group to another. In addition, the individual can combine all the ideas he or she receives from different sources and come up with the most innovative idea among all. At the same time, a broker also occupies a precarious position, as ties with disparate groups can be fragile and time consuming to maintain.

Two types of network structure

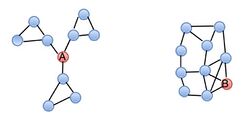
If we compare two nodes, node A is more likely to get novel information than node B, even though they have the same number of links. This is so because nodes connected to B are also highly connected between each other. Therefore, any information that any of them could get from B, it could easily get from other nodes as well. Furthermore, the information, which B gets from different connections, is likely to be overlapping, so connections involving node B are said to be redundant. On contrary, the position of node A makes it serve as a bridge or a ‘broker’ between three different clusters. Thus, node A is likely to receive some non-redundant information from its contacts. The term ‘structural holes’ is used for the separation between non-redundant contacts. As a result of the hole between two contacts, they provide network benefits to the third party (to node A).

Measures

Bridge counts

Bridge count is a simple and intuitive measure of structural holes in a network. Bridge is defined as a relation between two individuals if there is no indirect connection between them through mutual contacts.

Effective size

Burt's formula

Burt introduced the measure of a network’s redundancy. He aims to estimate to what extent contact j is redundant with other contacts of node i. Redundancy is understood as an investment of time and energy in a relationship with another node q, with whom node j is strongly connected.

[math]\displaystyle{ \text{Redundancy}=p_{iq}m_{jq} }[/math]

Where p_iq is proportion of i’s energy invested in relationship with q,

And m_jq is calculated as j’s interaction with q divided by j’s strongest relationship with anyone.

The redundancy in network is calculated by summing up this product across all nodes q. One minus this expression expresses the non-redundant portion of relationship. Effective size of i’s network is defined as a sum of the j’s nonredundant contacts.

[math]\displaystyle{ \text{Effective size of i's network}=\sum_j\left[1-\sum_qp_{iq}m_{jq} \right ],\quad q\neq i,j, }[/math]

The more each node is disconnected from other primary contacts, the higher the effective size would be. This indicator varies from 1 (network only provides a single link) to the total number of links N (each contact is non-redundant).

Borgatti's reformulation of Burt's formula

Borgatti developed a simplified formula to calculate effective size for unweighted networks.

[math]\displaystyle{ \text{Redundancy}=\frac{2t}{n} }[/math]

Where t is the number of the total ties in the egocentric network (excluding those ties to the ego) and n is the number of total nodes in the egocentric network (excluding the ego). This formula can be modified to calculate the effective size of the ego's network.

[math]\displaystyle{ \text{Effective size of ego's network}= n -\frac{2t}{n} }[/math]

Constraint

Network constraint of a network is a sum of each connection's constraints c_ij:

[math]\displaystyle{ c_{ij}=(p_{ij}+\sum_qp_{iq}p_{qj})^2,\quad i\neq q\neq j }[/math]

This indicator measures the extent to which time and energy is concentrated within a single cluster. It consists of two components: direct, when a contact consumes a large proportion of a network's time and energy, and indirect, when a contact controls other individuals, who consume a large proportion of a network's time and energy.

Network constraint measures the extent to which the manager’s network of colleagues is like a straitjacket around the manager, limiting his or her vision of alternative ideas and sources of support. It depends on three network characteristics: size, density, and hierarchy. Constraint on an individual would be generally higher in case of a small network (he or she has just few contacts), and if contacts are highly connected between each other (either directly as in a dense network, or indirectly, through the mutual central contact as in a hierarchical network).

Structural holes vs. Weak ties

The idea behind structural holes theory is somewhat close to the strength of weak ties theory, famously developed by Mark Granovetter. According to weak ties argument, the stronger the tie between two people is, the more likely their contacts will overlap so that they will have common ties with the same third parties. This implies that bridging ties are a potential source of novel ideas. Therefore, Granovetter argues that strong ties are unlikely to transfer any novel information.

Both concepts rely on the same underlying model, however, some differences between them can be distinguished. While Granovetter claims that whether a contact would serve as a bridge depends on a tie’s strength, Burt considers the opposite direction of causality. Thus, he prefers the proximal cause (bridging ties), while Granovetter argues in favor of the distal cause (strength of ties).

Applications

The networks rich in structural holes were referred to as entrepreneurial networks, and the individual who benefits from structural holes is considered as an entrepreneur. Application for this theory can be found in one of Burt's studies of entrepreneurial network. He studied a network of 673 managers in the supply chain for the firm, and measured the degree of social brokerage. All the managers had to submit their ideas about the ways to improve supply chain management, which were then evaluated by judges. The findings of this empirical study:

• An idea's value corresponded to the degree that the individuals were measured as social brokers;
• The wages of individuals corresponded to the degree that they were measured as social brokers;
• Managers who discussed issues with other managers were better paid, better evaluated positively, and more likely to be promoted.

There are several practical scenarios related to structural hole-related applications, including enterprise settings, information diffusion in social networks, software development, mobile applications, and machine learning (ML)-based social prediction.