Stuttering equivalence

In theoretical computer science, stuttering equivalence, a relation written as

The paths $\pi$ and ${\pi }^{\prime }$ are stuttering equivalent.

$\pi {\sim }_{st}{\pi }^{\prime }$,

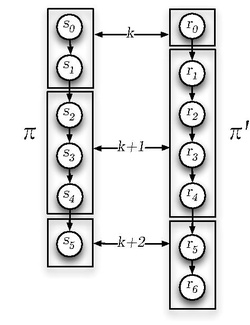
can be seen as a partitioning of paths $\pi$ and ${\pi }^{\prime }$ into blocks, so that states in the $k^{\mathrm{t}\mathrm{h}}$ block of one path are labeled ($L(\cdot )$) the same as states in the $k^{\mathrm{t}\mathrm{h}}$ block of the other path. Corresponding blocks may have different lengths.

Formally, this can be expressed as two infinite paths $\pi =s_0,s_1,\dots$ and ${\pi }^{\prime }=r_0,r_1,\dots$ being stuttering equivalent ($\pi {\sim }_{st}{\pi }^{\prime }$) if there are two infinite sequences of integers $0=i_0<i_1<i_2<\dots$ and $0=j_0<j_1<j_2<\dots$ such that for every block $k\ge 0$ holds $L(s_{i_k})=L(s_{i_k+1})=\dots =L(s_{i_{k+1}-1})=L(r_{j_k})=L(r_{j_k+1})=\dots =L(r_{j_{k+1}-1})$.

Stuttering equivalence is not the same as bisimulation, since bisimulation cannot capture the semantics of the 'eventually' (or 'finally') operator found in linear temporal/computation tree logic (branching time logic)(modal logic). So-called branching bisimulation has to be used.