Sum of two cubes
 |
In mathematics, the sum of two cubes is a cubed number added to another cubed number.
Factorization
Every sum of cubes may be factored according to the identity [math]\displaystyle{ a^3 + b^3 = (a + b)(a^2 - ab + b^2) }[/math] in elementary algebra.[1]
Binomial numbers are the general of this factorization to higher odd powers.
"SOAP" method
The mnemonic "SOAP", standing for "Same, Opposite, Always Positive", is sometimes used to memorize the correct placement of the addition and subtraction symbols while factorizing cubes.[2] When applying this method to the factorization, "Same" represents the first term with the same sign as the original expression, "Opposite" represents the second term with the opposite sign as the original expression, and "Always Positive" represents the third term and is always positive.
original
signSame Opposite Always
Positive[math]\displaystyle{ a^3 }[/math] [math]\displaystyle{ + }[/math] [math]\displaystyle{ b^3\quad=\quad(a }[/math] [math]\displaystyle{ + }[/math] [math]\displaystyle{ b)(a^2 }[/math] [math]\displaystyle{ - }[/math] [math]\displaystyle{ ab }[/math] [math]\displaystyle{ + }[/math] [math]\displaystyle{ b^2) }[/math] [math]\displaystyle{ a^3 }[/math] [math]\displaystyle{ - }[/math] [math]\displaystyle{ b^3\quad=\quad(a }[/math] [math]\displaystyle{ - }[/math] [math]\displaystyle{ b)(a^2 }[/math] [math]\displaystyle{ + }[/math] [math]\displaystyle{ ab }[/math] [math]\displaystyle{ + }[/math] [math]\displaystyle{ b^2) }[/math]
Proof
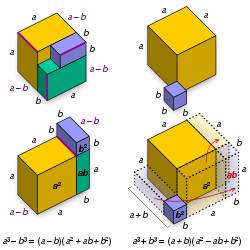
Starting with the expression, [math]\displaystyle{ a^2-ab+b^2 }[/math] is multiplied by a and b[1] [math]\displaystyle{ (a+b)(a^2-ab+b^2) = a(a^2-ab+b^2) + b(a^2-ab+b^2). }[/math] By distributing a and b to [math]\displaystyle{ a^2-ab+b^2 }[/math], one get[1] [math]\displaystyle{ a^3 - a^2 b + ab^2 + a^2b - ab^2 + b^3 }[/math] and by canceling the alike terms, one get[1] [math]\displaystyle{ a^3 + b^3. }[/math]
Similarly for the difference of cubes, [math]\displaystyle{ \begin{align} (a-b)(a^2+ab+b^2) & = a(a^2+ab+b^2) - b(a^2+ab+b^2) \\ & = a^3 + a^2 b + ab^2 \; - a^2b - ab^2 - b^3 \\ & = a^3 - b^3. \end{align} }[/math]
Fermat's last theorem
Fermat's last theorem in the case of exponent 3 states that the sum of two non-zero integer cubes does not result in a non-zero integer cube. The first recorded proof of the exponent 3 case was given by Euler.[3]
Taxicab and Cabtaxi numbers
Taxicab numbers are numbers that can be expressed as a sum of two positive integer cubes in n distinct ways. The smallest taxicab number, after Ta(1), is 1729,[4] expressed as
- [math]\displaystyle{ 1^3 +12^3 }[/math] or [math]\displaystyle{ 9^3 + 10^3 }[/math]
The smallest taxicab number expressed in 3 different ways is 87,539,319, expressed as
- [math]\displaystyle{ 436^3 + 167^3 }[/math], [math]\displaystyle{ 423^3 + 228^3 }[/math] or [math]\displaystyle{ 414^3 + 255^3 }[/math]
Cabtaxi numbers are numbers that can be expressed as a sum of two positive or negative integers or 0 cubes in n ways. The smallest cabtaxi number, after Cabtaxi(1), is 91,[5] expressed as:
- [math]\displaystyle{ 3^3 + 4^3 }[/math] or [math]\displaystyle{ 6^3 - 5^3 }[/math]
The smallest Cabtaxi number expressed in 3 different ways is 4104,[6] expressed as
- [math]\displaystyle{ 16^3 + 2^3 }[/math], [math]\displaystyle{ 15^3 + 9^3 }[/math] or [math]\displaystyle{ -12^3+18^3 }[/math]
See also
- Difference of two squares
- Binomial number
- Sophie Germain's identity
- Aurifeuillean factorization
- Fermat's last theorem
References
- ↑ 1.0 1.1 1.2 1.3 McKeague, Charles P. (1986). Elementary Algebra (3rd ed.). Academic Press. p. 388. ISBN 0-12-484795-1. https://books.google.com/books?id=sq7iBQAAQBAJ&pg=PA388.
- ↑ Kropko, Jonathan (2016). Mathematics for social scientists. Los Angeles, LA: Sage. p. 30. ISBN 9781506304212.
- ↑ Dickson, L. E. (1917). "Fermat's Last Theorem and the Origin and Nature of the Theory of Algebraic Numbers". Annals of Mathematics 18 (4): 161–187. doi:10.2307/2007234. ISSN 0003-486X.
- ↑ "A001235 - OEIS". https://oeis.org/A001235.
- ↑ Schumer, Peter (2008). "Sum of Two Cubes in Two Different Ways". Math Horizons 16 (2): 8–9. https://www.jstor.org/stable/25678781.
- ↑ Silverman, Joseph H. (1993). "Taxicabs and Sums of Two Cubes". The American Mathematical Monthly 100 (4): 331–340. doi:10.2307/2324954. ISSN 0002-9890.
Further reading
- Broughan, Kevin A. (January 2003). "Characterizing the Sum of Two Cubes". Journal of Integer Sequences 6 (4): 46. Bibcode: 2003JIntS...6...46B. https://cs.uwaterloo.ca/journals/JIS/VOL6/Broughan/broughan25.pdf.
 |  |
