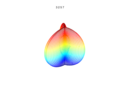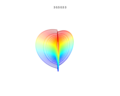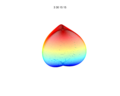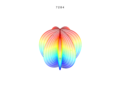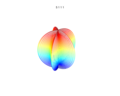Superformula

The superformula is a generalization of the superellipse and was proposed by Johan Gielis around 2000. Gielis suggested that the formula can be used to describe many complex shapes and curves that are found in nature. Gielis has filed a patent application related to the synthesis of patterns generated by the superformula, which expired effective 2020-05-10.

In polar coordinates, with [math]\displaystyle{ r }[/math] the radius and [math]\displaystyle{ \varphi }[/math] the angle, the superformula is:

[math]\displaystyle{ r\left(\varphi\right) = \left( \left| \frac{\cos\left(\frac{m\varphi}{4}\right)}{a} \right| ^{n_2} + \left| \frac{\sin\left(\frac{m\varphi}{4}\right)}{b} \right| ^{n_3} \right) ^{-\frac{1}{n_{1}}}. }[/math] By choosing different values for the parameters [math]\displaystyle{ a, b, m, n_1, n_2, }[/math] and [math]\displaystyle{ n_3, }[/math] different shapes can be generated.

The formula was obtained by generalizing the superellipse, named and popularized by Piet Hein, a Denmark mathematician.

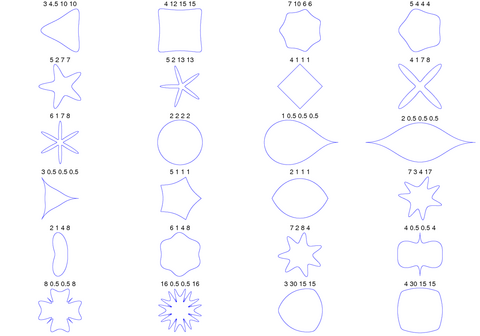
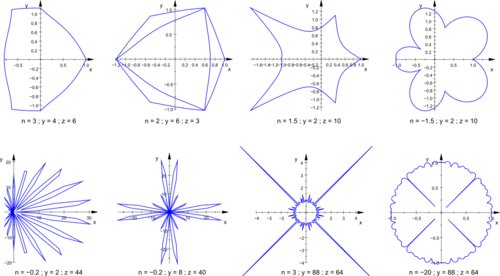
2D plots

In the following examples the values shown above each figure should be m, n₁, n₂ and n₃.

A GNU Octave program for generating these figures

function sf2d(n, a)
  u = [0:.001:2 * pi];
  raux = abs(1 / a(1) .* abs(cos(n(1) * u / 4))) .^ n(3) + abs(1 / a(2) .* abs(sin(n(1) * u / 4))) .^ n(4);
  r = abs(raux) .^ (- 1 / n(2));
  x = r .* cos(u);
  y = r .* sin(u);
  plot(x, y);
end

Extension to higher dimensions

It is possible to extend the formula to 3, 4, or n dimensions, by means of the spherical product of superformulas. For example, the 3D parametric surface is obtained by multiplying two superformulas r₁ and r₂. The coordinates are defined by the relations:

[math]\displaystyle{ x = r_1(\theta)\cos\theta \cdot r_2(\phi)\cos\phi, }[/math] [math]\displaystyle{ y = r_1(\theta)\sin\theta \cdot r_2(\phi)\cos\phi, }[/math] [math]\displaystyle{ z = r_2(\phi)\sin\phi, }[/math]

where [math]\displaystyle{ \phi }[/math] (latitude) varies between −π/2 and π/2 and θ (longitude) between −π and π.

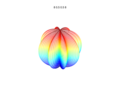
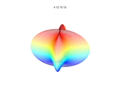
3D plots

3D superformula: a = b = 1; m, n₁, n₂ and n₃ are shown in the pictures.

• 
• 
• 
• 
• 
• 
• 
• 

A GNU Octave program for generating these figures:

function sf3d(n, a)
  u = [- pi:.05:pi];
  v = [- pi / 2:.05:pi / 2];
  nu = length(u);
  nv = length(v);
  for i = 1:nu
    for j = 1:nv
      raux1 = abs(1 / a(1) * abs(cos(n(1) .* u(i) / 4))) .^ n(3) + abs(1 / a(2) * abs(sin(n(1) * u(i) / 4))) .^ n(4);
      r1 = abs(raux1) .^ (- 1 / n(2));
      raux2 = abs(1 / a(1) * abs(cos(n(1) * v(j) / 4))) .^ n(3) + abs(1 / a(2) * abs(sin(n(1) * v(j) / 4))) .^ n(4);
      r2 = abs(raux2) .^ (- 1 / n(2));
      x(i, j) = r1 * cos(u(i)) * r2 * cos(v(j));
      y(i, j) = r1 * sin(u(i)) * r2 * cos(v(j));
      z(i, j) = r2 * sin(v(j));
    endfor;
  endfor;
  mesh(x, y, z);
endfunction;

Generalization

The superformula can be generalized by allowing distinct m parameters in the two terms of the superformula. By replacing the first parameter [math]\displaystyle{ m }[/math] with y and second parameter [math]\displaystyle{ m }[/math] with z: [math]\displaystyle{ r\left(\varphi\right) = \left( \left| \frac{\cos\left(\frac{y\varphi}{4}\right)}{a} \right| ^{n_2} + \left| \frac{\sin\left(\frac{z\varphi}{4}\right)}{b} \right| ^{n_3} \right) ^{-\frac{1}{n_{1}}} }[/math]

This allows the creation of rotationally asymmetric and nested structures. In the following examples a, b, [math]\displaystyle{ {n_2} }[/math] and [math]\displaystyle{ {n_3} }[/math] are 1:

External links

• Some Experiments on Fitting of Gielis Curves by Simulated Annealing and Particle Swarm Methods of Global Optimization
• Least Squares Fitting of Chacón-Gielis Curves By the Particle Swarm Method of Optimization
• Superformula 2D Plotter & SVG Generator
• Interactive example using JSXGraph
• SuperShaper: An OpenSource, OpenCL accelerated, interactive 3D SuperShape generator with shader based visualisation (OpenGL3)
• Simpel, WebGL based SuperShape implementation