Swirl function

In mathematics, swirl functions are special functions defined as follows：

[math]\displaystyle{ S(k,n,r,\theta)=\sin(k\cos(r) -n\theta) }[/math]

where k and n are integers, and r and θ are polar coordinates.

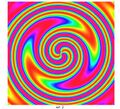
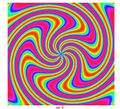
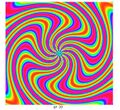
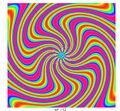
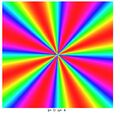
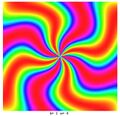
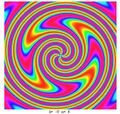
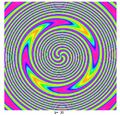
When these functions are graphed, they usually resemble a swirling fan blade, where n is the number of blades, k is related to the shape of each blade.

Symmetry

The function S(k,n,r,θ) satisfies the following relations:

mirror symmetry

• [math]\displaystyle{ f(-k, n, r, \theta)=-f(k, n, r, -\theta) }[/math]
• [math]\displaystyle{ f(-k, n, r, \theta)=-f(k, -n, r, \theta) }[/math]
• [math]\displaystyle{ f(-k, -n, r, \theta)=-f(k, n, r, \theta) }[/math]
• [math]\displaystyle{ f(-k, n, r, -\theta)=-f(k, n, r, \theta) }[/math]
• [math]\displaystyle{ f(-k, n, r, \theta)=-f(k, n, -r, -\theta) }[/math]
• [math]\displaystyle{ f(-k, n, -r, -\theta)=-f(k, n, r, \theta) }[/math]
• [math]\displaystyle{ f(-k, -n, -r, \theta)=-f(k, n, r, \theta) }[/math]
• [math]\displaystyle{ f(-k, n, -r, -\theta)=-f(k, n, r, \theta) }[/math]

full symmetry

• [math]\displaystyle{ f(k, -n, r, \theta)=f(k, n, r, -\theta) }[/math]
• [math]\displaystyle{ f(k, -n, r, -\theta)=f(k, n, r, \theta) }[/math]
• [math]\displaystyle{ f(k, n, -r, \theta)=f(k, n, r, \theta) }[/math]
• [math]\displaystyle{ f(k, n, -r, \theta)=f(k, n, r, \theta) }[/math]
• [math]\displaystyle{ f(k, n, -r, \theta)=f(k, -n, r, -\theta) }[/math]
• [math]\displaystyle{ f(k, -n, -r, -\theta)=f(k, n, r, \theta) }[/math]
• [math]\displaystyle{ f(k, n, -r, \theta)-f(k, n, r, \theta) }[/math]

rotation symmetry

[math]\displaystyle{ S\left(k,n,r,\theta+\frac{2\pi}{n}\right)=S(k,n,r,\theta) }[/math]

examples

First number is n, second is k

• 

  7,-2

• 

  7,2

• 

  7,-4

• 

  7,4

• 

  7,-6

• 

  7,6

• 

  7,-8

• 

  7,8

• 

  7,-10

• 

  7,10

• 

  7,-12

• 

  7,12

• 

  0,4

• 

  1,4

• 

  2,4

• 

  7,4

• 

  -5,4

• 

  -9,4

• 

  30,4