Ring counter
A ring counter is a type of counter composed of flip-flops connected into a shift register, with the output of the last flip-flop fed to the input of the first, making a "circular" or "ring" structure.
There are two types of ring counters:
- A straight ring counter, also known as a one-hot counter, connects the output of the last shift register to the first shift register input and circulates a single one (or zero) bit around the ring.
- A twisted ring counter, also called switch-tail ring counter, walking ring counter, Johnson counter, or Möbius counter, connects the complement of the output of the last shift register to the input of the first register and circulates a stream of ones followed by zeros around the ring.
Four-bit ring-counter sequences
| Straight ring counter | Johnson counter | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| State | Q0 | Q1 | Q2 | Q3 | State | Q0 | Q1 | Q2 | Q3 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | |
| 2 | 0 | 0 | 1 | 0 | 2 | 1 | 1 | 0 | 0 | |
| 3 | 0 | 0 | 0 | 1 | 3 | 1 | 1 | 1 | 0 | |
| 0 | 1 | 0 | 0 | 0 | 4 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 1 | 0 | 0 | 5 | 0 | 1 | 1 | 1 | |
| 2 | 0 | 0 | 1 | 0 | 6 | 0 | 0 | 1 | 1 | |
| 3 | 0 | 0 | 0 | 1 | 7 | 0 | 0 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
Properties
Ring counters are often used in hardware design (e.g. ASIC and FPGA design) to create finite-state machines. A binary counter would require an adder circuit which is substantially more complex than a ring counter and has higher propagation delay as the number of bits increases, whereas the propagation delay of a ring counter will be nearly constant regardless of the number of bits in the code.
The straight and twisted forms have different properties, and relative advantages and disadvantages.
A general disadvantage of ring counters is that they are lower density codes than normal binary encodings of state numbers. A binary counter can represent 2N states, where N is the number of bits in the code, whereas a straight ring counter can represent only N states and a Johnson counter can represent only 2N states. This may be an important consideration in hardware implementations where registers are more expensive than combinational logic.
Johnson counters are sometimes favored, because they offer twice as many count states from the same number of shift registers, and because they are able to self-initialize from the all-zeros state, without requiring the first count bit to be injected externally at start-up. The Johnson counter generates a code in which adjacent states differ by only one bit (that is, have a Hamming distance of 1), as in a Gray code, which can be useful if the bit pattern is going to be asynchronously sampled.[1]
When a fully decoded or one-hot representation of the counter state is needed, as in some sequence controllers, the straight ring counter is preferred. The one-hot property means that the set of codes are separated by a minimum Hamming distance of 2,[2] so any single-bit error is detectable (as is any error pattern other than turning on one bit and turning off one bit).
Sometimes bidirectional shift registers are used (using multiplexors to take the input for each flip-flop from its left or right neighbor), so that bidirectional or up–down ring counters can be made.[3]
Logic diagrams
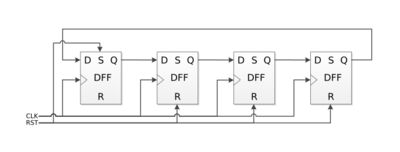
The straight ring counter has the logical structure shown here:
Instead of the reset line setting up the initial one-hot pattern, the straight ring is sometimes made self-initializing by the use of a distributed feedback gate across all of the outputs except that last, so that a 1 is presented at the input when there is no 1 in any stage but the last.[4]
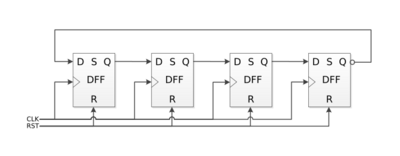
A Johnson counter, named for Robert Royce Johnson, is a ring with an inversion; here is a 4-bit Johnson counter:
Note the small bubble indicating inversion of the Q signal from the last shift register before feeding back to the first D input, making this a Johnson counter.
History
Before the days of digital computing, digital counters were used to measure rates of random events such as radioactive decays to alpha and beta particle. Fast "pre-scaling" counters reduced the rate of random events to more manageable and more regular rates. Five-state ring counters were used along with divide-by-two scalers to make decade (power-of-ten) scalers before 1940, such as those developed by C. E. Wynn-Williams.[5]
Early ring counters used only one active element (vacuum tube, valve, or transistor) per stage, relying on global feedback rather than local bistable flip-flops, to suppress states other than the one-hot states, for example in the 1941 patent filing of Robert E. Mumma of the National Cash Registor Company.[6] Wilcox P. Overbeck invented a version using multiple anodes in a single vacuum tube,[7][8] In recognition of his work, ring counters are sometimes referred to as "Overbeck rings"[9][10] (and after 2006, sometimes as "Overbeck counters", since Wikipedia used that term from 2006 to 2018).
The ENIAC used decimal arithmetic based on 10-state one-hot ring counters. The works of Mumma at NCR and Overbeck at MIT were among the prior art works examined by the patent office in invalidated the patents of J. Presper Eckert and John Mauchly for the ENIAC technology.[11]
By the 1950s, ring counters with a two-tube or twin-triode flip-flop per stage were appearing.[12]
Robert Royce Johnson developed a number of different shift-register-based counters with the aim of making different numbers of states with the simplest possible feedback logic, and filed for a patent in 1953.[13] The Johnson counter is the simplest of these.
Applications
Early applications of ring counters were as frequency prescalers (e.g. for Geiger counter and such instruments),[5] as counters to count pattern occurrences in cryptanalysis (e.g. in the Heath Robinson codebreaking machine and the Colossus computer),[14] and as accumulator counter elements for decimal arithmetic in computers and calculators, using either bi-quinary (as in the Colossus) or ten-state one-hot (as in the ENIAC) representations.
Straight ring counters generate fully decoded one-hot codes to that are often used to enable a specific action in each state of a cyclic control cycle. One-hot codes can also be decoded from a Johnson counter, using one gate for each state.[15][nb 1]
Besides being an efficient alternative way to generate one-hot codes and frequency pre-scalers, a Johnson counter is also a simple way to encode a cycle of an even number of states that can be asynchronously sampled without glitching, since only one bit changes at a time, as in a Gray code.[16] Early computer mice used up–down (bidirectional) 2-bit Johnson or Gray encodings to indicate motion in each of the two dimensions, though in mice those codes were not usually generated by rings of flip-flops (but instead by electro-mechanical or optical quadrature encoders).[17] A 2-bit Johnson code and a 2-bit Gray code are identical, while for 3 or more bits Gray and Johnson codes are different. In the 5-bit case, the code is the same as the Libaw–Craig code (de) for decimal digits.[18][19][20][21][22][23][24][25]
A walking ring counter, also called a Johnson counter, and a few resistors can produce a glitch-free approximation of a sine wave. When combined with an adjustable prescaler, this is perhaps the simplest numerically-controlled oscillator. Two such walking ring counters are perhaps the simplest way to generate the continuous-phase frequency-shift keying used in dual-tone multi-frequency signaling and early modem tones.[26]
|
|
|
|
|
|
|
|
See also
Notes
- ↑ Johnson counter circuits with single states decoded in this way can be found in the original IBM MDA and CGA video display adapter designs, in the timing sequencer logic: one or two 74x174 hex D-type flip-flop ICs are wired as a shift register, fed back with inversion to form a Johnson counter, and 2-input NAND gates (in the MDA) or XOR gates (in the CGA) are used to decode states used as signals such as +RAS (Row Address Strobe [to DRAM]) and S/-L (Shift / NOT Load). Source: IBM Personal Computer Options & Adapters Technical Reference, Monochrome Display and Printer Adapter, logic diagrams; IBM Personal Computer Options & Adapters Technical Reference, Color Graphics Monitor Adapter, logic diagrams.
References
- ↑ Finite State Machines in Hardware: Theory and Design. MIT Press. 2013. p. 50. ISBN 978-0-26201966-8. https://books.google.com/books?id=SSkTDgAAQBAJ&pg=PA50.
- ↑ "State Encoding for Low-Power FSMs in FPGA". Integrated Circuit and System Design. Power and Timing Modeling, Optimization and Simulation: Proceedings of the 13th International Workshop, PATMOS 2003, Torino, Italy, 10–12 September 2003. 13. Springer Science & Business Media. 2003. p. 35. ISBN 9783540200741. https://books.google.com/books?id=JEEmfObxnrAC&pg=PA35.
- ↑ "Synchronous up/down counter with clock period independent of counter size". Proceedings 13th IEEE Symposium on Computer Arithmetic: 274–281. 1997. http://www.acsel-lab.com/arithmetic/arith13/papers/ARITH13_Stan.pdf.
- ↑ Digital Logic Design (4 ed.). Newnes Books / Elsevier Science. 2002. pp. 191–192. ISBN ((0-7506-4588-2)). https://books.google.com/books?id=o7enSwSVvgYC&pg=PA192. Retrieved 2020-04-19. (519 pages) [1]
- ↑ 5.0 5.1 Electrical Counting: With Special Reference to Counting Alpha and Beta Particles. Cambridge University Press. 1942. p. 90. ISBN 9781316611760. https://books.google.com/books?id=5B5CDAAAQBAJ&pg=PA90.
- ↑ "Electronic accumulation", Robert E. Mumma's US Patent No. 2405096, filed in 1941
- ↑ "Electronic switching device", Wilcox P. Overbeck's US Patent No. 2427533, filed in 1943
- ↑ Dayton Codebreakers: 1942 Research Report, mentioning "A new high speed counter by Mr. Overbeck, January 8, 1942"
- ↑ RAMAC 305 - IBM Customer Engineering Manual of Instruction. IBM. 1959. http://www.ed-thelen.org/RAMAC/IBM-227-3534-0-305-RAMAC-r.pdf. "[…] The Overbeck ring is used to supply timed pulses within computer circuits much as cam operated circuit breakers supply timed pulses on mechanical machines. It consists of a set of triggers with a common input from the ring drive line which carries pulses supplied by the process drum. […] Initially the triggers are reset OFF with the exception of the home trigger, which is ON. Each negative input pulse will turn OFF the trigger that is ON. The fall of the voltage at pin 10 of the trigger being turned OFF will grid flip the next trigger ON. This continues through a closed ring […]"
- ↑ Electrical Technology - A Suggested 2-Year Post High School Curriculum. Technical Education Program Series. United States, Division of Vocational and Technical Education. 1960. p. 52. https://books.google.com/books?id=0zoUAAAAIAAJ&q=%22overbeck+ring%22.
- ↑ Metropolis, Nicholas, ed (2014). "The Origins of Digital Computers: Supplementary Bibliography". History of Computing in the Twentieth Century. Elsevier. pp. 651–652. ISBN 9781483296685. https://books.google.com/books?id=AsvSBQAAQBAJ&pg=PA652.
- ↑ William Alfred Higinbotham, "Fast impulse circuits", US Patent No. 2536808, filed in 1949
- ↑ Robert Royce Johnson, "Electronic counter", US Patent No. 3030581, filed in 1953
- ↑ Colossus: The Secrets of Bletchley Park's Code-breaking Computers. Oxford University Press. 2010. pp. 123–128. ISBN 978-0-19957814-6.
- ↑ Foundations of Digital Logic Design. World Scientific. 1998. pp. 525–526. ISBN 978-9-81023110-1. https://books.google.com/books?id=4sX9fTGRo7QC&pg=PA525.
- ↑ "Digital dividers with symmetrical outputs - The author uses Johnson counters with controlled feedback to give symmetrical even and odd-numbered divisions of a clock pulse.". Wireless World (Sutton, Surrey, UK: IPC Business Press Ltd.) 88 (1559): 43–46. August 1982. ISSN 0043-6062. https://worldradiohistory.com/hd2/IDX-UK/Technology/Technology-All-Eras/Archive-Wireless-World-IDX/80s/Wireless-World-1982-08-OCR-Page-0024.pdf. Retrieved 2021-02-20. [2] [3] (4 pages)
- ↑ The Optical Mouse, and an Architectural Methodology for Smart Digital Sensors, Palo Alto Research Center, Palo Alto, California, USA: Xerox Corporation, August 1981, VLSI 81-1, http://www.bitsavers.org/pdf/xerox/parc/techReports/VLSI-81-1_The_Optical_Mouse.pdf, retrieved 2020-05-23, "The counters needed for X and Y simply count through four states, in either direction (up or down), changing only one bit at a time (i.e., 00, 01, 11, 10). This is a simple case of either a Gray-code counter or a Johnson counter (Moebius counter)." (41 pages)
- ↑ "A Photoelectric Decimal-Coded Shaft Digitizer". Transactions of the I.R.E. Professional Group on Electronic Computers EC-2 (3): 1–4. October 1953. doi:10.1109/IREPGELC.1953.5407731. ISSN 2168-1740. https://www.researchgate.net/publication/224112055. Retrieved 2020-05-26. (4 pages)
- ↑ "Codes particularly useful for analogue to digital conversions". A short note on useful codes for Fluidic Control Circuits. Cranfield, UK: The College of Aeronautics, Department of Production Engineering. June 1968. p. 10. CoA Memo 156. https://dspace.lib.cranfield.ac.uk/bitstream/handle/1826/9559/COA_Memo_156_June_1968.pdf. Retrieved 2020-12-15. (18 pages) (NB. The paper names the Glixon code modified Gray code and misspells Richard W. Hamming's name.)
- ↑ Digital Electronics. Philips Technical Library (PTL) / Macmillan Education (Reprint of 1st English ed.). Eindhoven, Netherlands: The Macmillan Press Ltd. / N. V. Philips' Gloeilampenfabrieken. 1973-06-18. p. 43. doi:10.1007/978-1-349-01417-0. ISBN 978-1-349-01419-4. https://books.google.com/books?id=hlRdDwAAQBAJ. Retrieved 2020-05-11. (270 pages)
- ↑ (in de) Digitale Elektronik in der Meßtechnik und Datenverarbeitung: Theoretische Grundlagen und Schaltungstechnik. Philips Fachbücher. I (improved and extended 5th ed.). Hamburg, Germany: Deutsche Philips GmbH. 1975. pp. 52, 58, 98. ISBN 3-87145-272-6. (xii+327+3 pages)
- ↑ (in de) Digitale Elektronik in der Meßtechnik und Datenverarbeitung: Anwendung der digitalen Grundschaltungen und Gerätetechnik. Philips Fachbücher. II (4th ed.). Hamburg, Germany: Deutsche Philips GmbH. 1975. p. 169. ISBN 3-87145-273-4. (xi+393+3 pages)
- ↑ Steinbuch, Karl W., ed (1962). written at Karlsruhe, Germany (in de). Taschenbuch der Nachrichtenverarbeitung (1 ed.). Berlin / Göttingen / New York: Springer-Verlag OHG. pp. 71–72, 74.
- ↑ (in de) Taschenbuch der Nachrichtenverarbeitung (2 ed.). Berlin, Germany: Springer-Verlag OHG. 1967. Title No. 1036.
- ↑ (in de) Taschenbuch der Informatik – Band II – Struktur und Programmierung von EDV-Systemen. 2 (3 ed.). Berlin, Germany: Springer Verlag. 1974. ISBN 3-540-06241-6.
- ↑ Don Lancaster. "TV Typewriter Cookbook". (TV Typewriter). 1976. p. 180-181.
 |