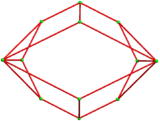
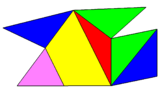
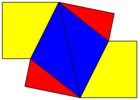
Ten of diamonds decahedron
| Ten of diamonds decahedron | |
|---|---|
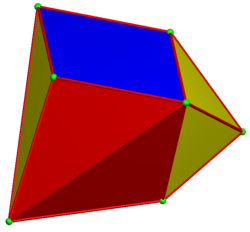 | |
| Faces | 8 triangles 2 rhombi |
| Edges | 16 |
| Vertices | 8 |
| Symmetry group | D2d, order 8 |
| Dual polyhedron | Skew-truncated tetragonal disphenoid |
| Properties | space-filling |
| Net | |
 | |
In geometry, the ten-of-diamonds decahedron is a space-filling polyhedron with 10 faces, 2 opposite rhombi with orthogonal major axes, connected by 8 identical isosceles triangle faces. Michael Goldberg references it by the playing card name, ten-of-diamonds, as a 10-faced polyhedron with two opposite rhombic (diamond-shaped) faces. He catalogued it in a 1982 paper as 10-II, the second in a list of 26 known space-filling decahedra.[1]
Coordinates
If the space-filling polyhedron is placed in a 3-D coordinate grid, the coordinates for the 8 vertices can be given as: (0, ±2, −1), (±2, 0, 1), (±1, 0, −1), (0, ±1, 1).
Symmetry
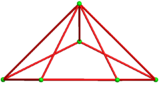
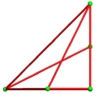
The ten-of-diamonds has D2d symmetry, which projects as order-4 dihedral (square) symmetry in two dimensions. It can be seen as a triakis tetrahedron, with two pairs of coplanar triangles merged into rhombic faces. The dual is similar to a truncated tetrahedron, except two edges from the original tetrahedron are reduced to zero length making pentagonal faces. The dual polyhedra can be called a skew-truncated tetragonal disphenoid, where 2 edges along the symmetry axis completely truncated down to the edge midpoint.
| Ten of diamonds | Related | Dual | Related | ||
|---|---|---|---|---|---|
 Solid faces |
 Edges |
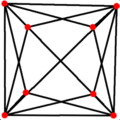 triakis tetrahedron |
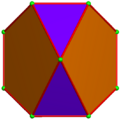 Solid faces |
 Edges |
 Truncated tetrahedron |
| v=8, e=16, f=10 | v=8, e=18, f=12 | v=10, e=16, f=8 | v=12, e=18, f=8 | ||
Honeycomb
| Ten of diamonds honeycomb | |
|---|---|
| Schläfli symbol | dht1,2{4,3,4} |
| Coxeter diagram | |
| Cell type | Ten-of-diamonds
|
| Space Fibrifold Coxeter |
I3 (204) 8−o 4,3+,4 |
| Dual | Alternated bitruncated cubic honeycomb |
| Properties | Cell-transitive |
The ten-of-diamonds is used in the honeycomb with Coxeter diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]() , being the dual of an alternated bitruncated cubic honeycomb,
, being the dual of an alternated bitruncated cubic honeycomb, ![]()
![]()
![]()
![]()
![]()
![]()
![]() . Since the alternated bitruncated cubic honeycomb fills space by pyritohedral icosahedra,
. Since the alternated bitruncated cubic honeycomb fills space by pyritohedral icosahedra, ![]()
![]()
![]()
![]()
![]() , and tetragonal disphenoidal tetrahedra, vertex figures of this honeycomb are their duals – pyritohedra,
, and tetragonal disphenoidal tetrahedra, vertex figures of this honeycomb are their duals – pyritohedra, ![]()
![]()
![]()
![]()
![]() and tetragonal disphenoids.
and tetragonal disphenoids.
Cells can be seen as the cells of the tetragonal disphenoid honeycomb, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , with alternate cells removed and augmented into neighboring cells by a center vertex. The rhombic faces in the honeycomb are aligned along 3 orthogonal planes.
, with alternate cells removed and augmented into neighboring cells by a center vertex. The rhombic faces in the honeycomb are aligned along 3 orthogonal planes.
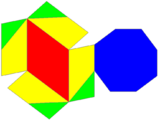
| Uniform | Dual | Alternated | Dual alternated | |
|---|---|---|---|---|
t1,2{4,3,4} |
dt1,2{4,3,4} |
ht1,2{4,3,4} |
dht1,2{4,3,4} | |
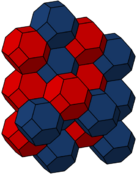 Bitruncated cubic honeycomb of truncated octahedral cells |
 tetragonal disphenoid honeycomb |
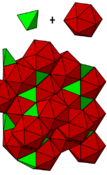 Dual honeycomb of icosahedra and tetrahedra Dual honeycomb of icosahedra and tetrahedra
|
 Ten-of-diamonds honeycomb |
 Honeycomb structure orthogonally viewed along cubic plane |
Related space-filling polyhedra
The ten-of-diamonds can be dissected in an octagonal cross-section between the two rhombic faces. It is a decahedron with 12 vertices, 20 edges, and 10 faces (4 triangles, 4 trapezoids, 1 rhombus, and 1 isotoxal octagon). Michael Goldberg labels this polyhedron 10-XXV, the 25th in a list of space-filling decahedra.[2]
The ten-of-diamonds can be dissected as a half-model on a symmetry plane into a space-filling heptahedron with 6 vertices, 11 edges, and 7 faces (6 triangles and 1 trapezoid). Michael Goldberg identifies this polyhedron as a triply truncated quadrilateral prism, type 7-XXIV, the 24th in a list of heptagonal space-fillers.[3]
It can be further dissected as a quarter-model by another symmetry plane into a space-filling hexahedron with 6 vertices, 10 edges, and 6 faces (4 triangles, 2 right trapezoids). Michael Goldberg identifies this polyhedron as an ungulated quadrilateral pyramid, type 6-X, the 10th in a list of space-filling hexahedron.[4]
Rhombic bowtie
| Rhombic bowtie | |
|---|---|
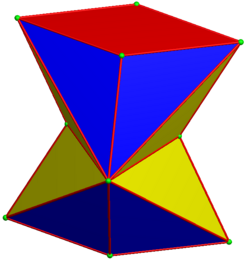 | |
| Faces | 16 triangles 2 rhombi |
| Edges | 28 |
| Vertices | 12 |
| Symmetry group | D2h, order 8 |
| Properties | space-filling |
| Net | |
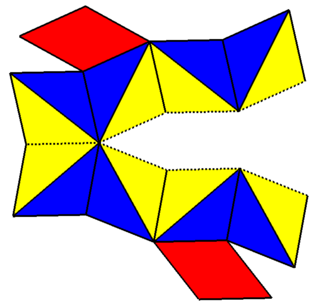 | |
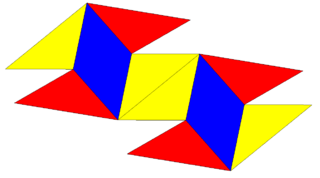
Pairs of ten-of-diamonds can be attached as a nonconvex bow-tie space-filler, called a rhombic bowtie for its cross-sectional appearance. The two right-most symmetric projections below show the rhombi edge-on on the top, bottom and a middle neck where the two halves are connected. The 2D projections can look convex or concave.
It has 12 vertices, 28 edges, and 18 faces (16 triangles and 2 rhombi) within D2h symmetry. These paired-cells stack more easily as inter-locking elements. Long sequences of these can be stacked together in 3 axes to fill space.[5]
The 12 vertex coordinates in a 2-unit cube. (further augmentations on the rhombi can be done with 2 unit translation in z.)
- (0, ±1, −1), (±1, 0, 0), (0, ±1, 1),
- (±1/2, 0, −1), (0, ±1/2, 0), (±1/2, 0, 1)
| Skew | Symmetric | |||
|---|---|---|---|---|
|
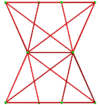
|
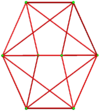
|
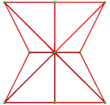
|
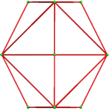
|
See also
References
- ↑ Goldberg, Michael. On the Space-filling Decahedra. Structural Topology, 1982, num. Type 10-II [1]
- ↑ On Space-filling Decahedra, type 10-XXV.
- ↑ Goldberg, Michael On the space-filling heptahedra Geometriae Dedicata, June 1978, Volume 7, Issue 2, pp 175–184 [2] PDF type 7-XXIV
- ↑ Goldberg, Michael On the space-filling hexahedra Geom. Dedicata, June 1977, Volume 6, Issue 1, pp 99–108 [3] PDF type 6-X
- ↑ Robert Reid, Anthony Steed Bowties: A Novel Class of Space Filling Polyhedron 2003
- Koch 1972 Koch, Elke, Wirkungsbereichspolyeder und Wirkungsbereichsteilunger zukubischen Gitterkomplexen mit weniger als drei Freiheitsgraden (Efficiency Polyhedra, and Efficiency Dividers, cubic lattice complexes with less than three degrees of freedom) Dissertation, University Marburg/Lahn 1972 - Model 10/8–1, 28–404.