Theorem of three moments

In civil engineering and structural analysis Clapeyron's theorem of three moments is a relationship among the bending moments at three consecutive supports of a horizontal beam. Let A,B,C-D be the three consecutive points of support, and denote by- l the length of AB and [math]\displaystyle{ l' }[/math] the length of BC, by w and [math]\displaystyle{ w' }[/math] the weight per unit of length in these segments. Then the bending moments [math]\displaystyle{ M_A,\, M_B,\, M_C }[/math] at the three points are related by:

[math]\displaystyle{ M_A l + 2 M_B (l+l') +M_C l' = \frac{1}{4} w l^3 + \frac{1}{4} w' (l')^3. }[/math]

This equation can also be written as

[math]\displaystyle{ M_A l + 2 M_B (l+l') +M_C l' = \frac{6 a_1 x_1}{l} + \frac{6 a_2 x_2}{l'} }[/math]

where a₁ is the area on the bending moment diagram due to vertical loads on AB, a₂ is the area due to loads on BC, x₁ is the distance from A to the centroid of the bending moment diagram of beam AB, x₂ is the distance from C to the centroid of the area of the bending moment diagram of beam BC.

The second equation is more general as it does not require that the weight of each segment be distributed uniformly.

Figure 01-Sample continuous beam section

Derivation of three moments equations

Mohr's theorem can be used to derive the three moment theorem (TMT).

Mohr's first theorem

The change in slope of a deflection curve between two points of a beam is equal to the area of the M/EI diagram between those two points.(Figure 02)

Figure 02-Mohr's First Theorem

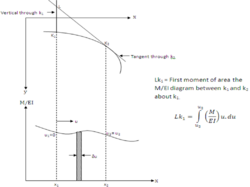
Mohr's second theorem

Consider two points k1 and k2 on a beam. The deflection of k1 and k2 relative to the point of intersection between tangent at k1 and k2 and vertical through k1 is equal to the moment of M/EI diagram between k1 and k2 about k1.(Figure 03)

Figure03-Mohr's Second Theorem

The three moment equation expresses the relation between bending moments at three successive supports of a continuous beam, subject to a loading on a two adjacent span with or without settlement of the supports.

The sign convention

According to the Figure 04,

1. The moment M1, M2, and M3 be positive if they cause compression in the upper part of the beam. (sagging positive)
2. The deflection downward positive. (Downward settlement positive)
3. Let ABC is a continuous beam with support at A,B, and C. Then moment at A,B, and C are M1, M2, and M3, respectively.
4. Let A' B' and C' be the final positions of the beam ABC due to support settlements.

Figure 04-Deflection Curve of a Continuous Beam Under Settlement

Derivation of three moment theorem

PB'Q is a tangent drawn at B' for final Elastic Curve A'B'C' of the beam ABC. RB'S is a horizontal line drawn through B'. Consider, Triangles RB'P and QB'S.

[math]\displaystyle{ \dfrac{PR}{RB'} = \dfrac{SQ}{B'S}, }[/math]

[math]\displaystyle{ \dfrac{PR}{L1} = \dfrac{SQ}{L2} }[/math]

(1)

[math]\displaystyle{ PR = \Delta B - \Delta A + PA' }[/math]

(2)

[math]\displaystyle{ SQ = \Delta C - \Delta B - QC' }[/math]

(3)

From (1), (2), and (3),

[math]\displaystyle{ \dfrac{\Delta B - \Delta A + PA'}{L1} = \dfrac{\Delta C - \Delta B - QC'}{L2} }[/math]

[math]\displaystyle{ \dfrac{PA'}{L1} + \dfrac{QC'}{L2} = \dfrac{\Delta A -\Delta B}{L1} + \dfrac{\Delta C -\Delta B}{L2} }[/math]

(a)

Draw the M/EI diagram to find the PA' and QC'.

Figure 05 - M / EI Diagram

From Mohr's Second Theorem
PA' = First moment of area of M/EI diagram between A and B about A.

[math]\displaystyle{ PA' = \left(\frac{1}{2} \times \frac{M_1}{E_1 I_1} \times L_1\right)\times L_1\times \frac{1}{3} + \left(\frac{1}{2} \times \frac{M_2}{E_2 I_2} \times L_1\right)\times L_1\times\frac{2}{3}+ \frac{A_1 X_1}{E_1 I_1} }[/math]

QC' = First moment of area of M/EI diagram between B and C about C.

[math]\displaystyle{ QC' = \left(\frac{1}{2} \times \frac{M_3}{E_2 I_2} \times L_2\right)\times L_2\times\frac{1}{3} + \left(\frac{1}{2} \times \frac{M_2}{E_2 I_2} \times L_2\right)\times L_2\times\frac{2}{3}+ \frac{A_2 X_2}{E_2 I_2} }[/math]

Substitute in PA' and QC' on equation (a), the Three Moment Theorem (TMT) can be obtained.

Three moment equation

[math]\displaystyle{ \frac{M_1 L_1}{E_1 I_1}+ 2M_2\left(\frac{L_1}{E_1 I_1} + \frac{L_2}{E_2 I_2}\right)+\frac{M_3 L_2}{E_2 I_2} = 6 [\frac{\Delta A - \Delta B}{L_1} + \frac{\Delta C - \Delta B}{L_2}] - 6 [\frac{A_1 X_1}{E_1 I_1 L_1} + \frac{A_2 X_2}{E_2 I_2 L_2}] }[/math]

External links

• CodeCogs: Continuous beams with more than one span