Thomsen's theorem

Short description: A certain path of line segments parallel to a triangle's edges ends at its starting point

Thomsen's theorem, [math]\displaystyle{ P_7=P_1 }[/math]

Thomsen's theorem, named after Gerhard Thomsen, is a theorem in elementary geometry. It shows that a certain path constructed by line segments being parallel to the edges of a triangle always ends up at its starting point.

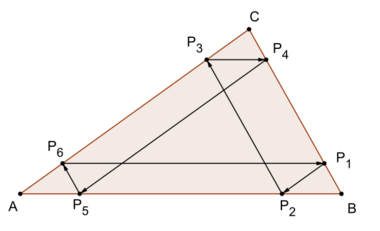
Consider an arbitrary triangle ABC with a point P₁ on its edge BC. A sequence of points and parallel lines is constructed as follows. The parallel line to AC through P₁ intersects AB in P₂ and the parallel line to BC through P₂ intersects AC in P₃. Continuing in this fashion the parallel line to AB through P₃ intersects BC in P₄ and the parallel line to AC through P₄ intersects AB in P₅. Finally the parallel line to BC through P₅ intersects AC in P₆ and the parallel line to AB through P₆ intersects BC in P₇. Thomsen's theorem now states that P₇ is identical to P₁ and hence the construction always leads to a closed path P₁P₂P₃P₄P₅P₆P₁

References

• Satz von Thomsen In: Schülerduden – Mathematik II. Bibliographisches Institut & F. A. Brockhaus, 2004, ISBN:3-411-04275-3, pp. 358–359 (German)

External links

• Darij Grinberg: Schließungssätze in der ebenen Geometrie (German)
• Weisstein, Eric W.. "Thomsen's Figure". http://mathworld.wolfram.com/ThomsensFigure.html.