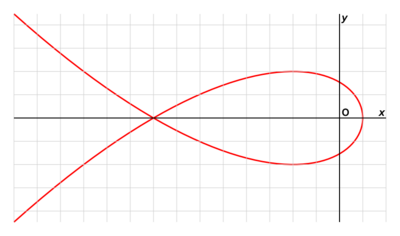
Tschirnhausen cubic
In algebraic geometry, the Tschirnhausen cubic, or Tschirnhaus' cubic is a plane curve defined, in its left-opening form, by the polar equation
- [math]\displaystyle{ r = a\sec^3 \left(\frac{\theta}{3}\right) }[/math]
where sec is the secant function.
History
The curve was studied by von Tschirnhaus, de L'Hôpital, and Catalan. It was given the name Tschirnhausen cubic in a 1900 paper by R C Archibald, though it is sometimes known as de L'Hôpital's cubic or the trisectrix of Catalan.
Other equations
Put [math]\displaystyle{ t=\tan(\theta/3) }[/math]. Then applying triple-angle formulas gives
- [math]\displaystyle{ x=a\cos \theta \sec^3 \frac{\theta}{3} = a \left(\cos^3 \frac{\theta}{3} - 3 \cos \frac{\theta}{3} \sin^2 \frac{\theta}{3} \right) \sec^3 \frac{\theta}{3}= a\left(1 - 3 \tan^2 \frac{\theta}{3}\right) }[/math]
- [math]\displaystyle{ = a(1 - 3t^2) }[/math]
- [math]\displaystyle{ y=a\sin \theta \sec^3 \frac{\theta}{3} = a \left(3 \cos^2 \frac{\theta}{3}\sin \frac{\theta}{3} - \sin^3 \frac{\theta}{3} \right) \sec^3 \frac{\theta}{3}= a \left(3 \tan \frac{\theta}{3} - \tan^3 \frac{\theta}{3} \right) }[/math]
- [math]\displaystyle{ = at(3-t^2) }[/math]
giving a parametric form for the curve. The parameter t can be eliminated easily giving the Cartesian equation
- [math]\displaystyle{ 27ay^2 = (a-x)(8a+x)^2 }[/math].
If the curve is translated horizontally by 8a and the signs of the variables are changed, the equations of the resulting right-opening curve are
- [math]\displaystyle{ x = 3a(3-t^2) }[/math]
- [math]\displaystyle{ y = at(3-t^2) }[/math]
and in Cartesian coordinates
- [math]\displaystyle{ x^3=9a \left(x^2-3y^2 \right) }[/math].
This gives the alternative polar form
- [math]\displaystyle{ r=9a \left(\sec \theta - 3\sec \theta \tan^2 \theta \right) }[/math].
Generalization
The Tschirnhausen cubic is a Sinusoidal spiral with n = −1/3.
References
- J. D. Lawrence, A Catalog of Special Plane Curves. New York: Dover, 1972, pp. 87-90.
External links
- Weisstein, Eric W.. "Tschirnhausen Cubic". http://mathworld.wolfram.com/TschirnhausenCubic.html.
- "Tschirnhaus' Cubic" at MacTutor History of Mathematics archive
- Tschirnhausen cubic at mathcurve.com