Type-1 OWA operators

Short description: Set of aggregation operators that generalise the Yager's OWA

Type-1 OWA operators are a set of aggregation operators that generalise the Yager's OWA (ordered weighted averaging) operators) in the interest of aggregating fuzzy sets rather than crisp values in soft decision making and data mining.

These operators provide a mathematical technique for directly aggregating uncertain information with uncertain weights via OWA mechanism in soft decision making and data mining, where these uncertain objects are modelled by fuzzy sets.

The two definitions for type-1 OWA operators are based on Zadeh's Extension Principle and [math]\displaystyle{ \alpha }[/math]-cuts of fuzzy sets. The two definitions lead to equivalent results.

Definitions

Definition 1

Let [math]\displaystyle{ F(X) }[/math] be the set of fuzzy sets with domain of discourse [math]\displaystyle{ X }[/math], a type-1 OWA operator is defined as follows:

Given n linguistic weights [math]\displaystyle{ \left\{ {W^i} \right\}_{i = 1}^n }[/math] in the form of fuzzy sets defined on the domain of discourse [math]\displaystyle{ U = [0,1] }[/math], a type-1 OWA operator is a mapping, [math]\displaystyle{ \Phi }[/math],

[math]\displaystyle{ \Phi \colon F(X)\times \cdots \times F(X) \longrightarrow F(X) }[/math]

[math]\displaystyle{ (A^1 , \cdots ,A^n) \mapsto Y }[/math]

such that

[math]\displaystyle{ \mu _{Y} (y) =\displaystyle \sup_{\displaystyle \sum_{k =1}^n \bar {w}_i a_{\sigma (i)} = y }\left({\begin{array}{*{1}l}\mu _{W^1 } (w_1 )\wedge \cdots \wedge \mu_{W^n } (w_n )\wedge \mu _{A^1 } (a_1 )\wedge \cdots \wedge \mu _{A^n } (a_n )\end{array}}\right) }[/math]

where [math]\displaystyle{ \bar {w}_i = \frac{w_i }{\sum_{i = 1}^n {w_i } } }[/math], and [math]\displaystyle{ \sigma \colon \{1, \cdots ,n\} \longrightarrow \{1, \cdots ,n\} }[/math] is a permutation function such that [math]\displaystyle{ a_{\sigma (i)} \geq a_{\sigma (i + 1)},\ \forall i = 1, \cdots ,n - 1 }[/math], i.e., [math]\displaystyle{ a_{\sigma(i)} }[/math] is the [math]\displaystyle{ i }[/math]th highest element in the set [math]\displaystyle{ \left\{ {a_1 , \cdots ,a_n } \right\} }[/math].

Definition 2

Using the alpha-cuts of fuzzy sets:

Given the n linguistic weights [math]\displaystyle{ \left\{ {W^i} \right\}_{i =1}^n }[/math] in the form of fuzzy sets defined on the domain of discourse [math]\displaystyle{ U = [0,\;\;1] }[/math], then for each [math]\displaystyle{ \alpha \in [0,\;1] }[/math], an [math]\displaystyle{ \alpha }[/math]-level type-1 OWA operator with [math]\displaystyle{ \alpha }[/math]-level sets [math]\displaystyle{ \left\{ {W_\alpha ^i } \right\}_{i = 1}^n }[/math] to aggregate the [math]\displaystyle{ \alpha }[/math]-cuts of fuzzy sets [math]\displaystyle{ \left\{ {A^i} \right\}_{i =1}^n }[/math] is:

[math]\displaystyle{ \Phi_\alpha \left( {A_\alpha ^1 , \ldots ,A_\alpha ^n } \right) =\left\{ {\frac{\sum\limits_{i = 1}^n {w_i a_{\sigma (i)} } }{\sum\limits_{i = 1}^n {w_i } }\left| {w_i \in W_\alpha ^i ,\;a_i } \right. \in A_\alpha ^i ,\;i = 1, \ldots ,n} \right\} }[/math]

where [math]\displaystyle{ W_\alpha ^i= \{w| \mu_{W_i }(w) \geq \alpha \}, A_\alpha ^i=\{ x| \mu _{A_i }(x)\geq \alpha \} }[/math], and [math]\displaystyle{ \sigma :\{\;1, \cdots ,n\;\} \to \{\;1, \cdots ,n\;\} }[/math] is a permutation function such that [math]\displaystyle{ a_{\sigma (i)} \ge a_{\sigma (i + 1)} ,\;\forall \;i = 1, \cdots ,n - 1 }[/math], i.e., [math]\displaystyle{ a_{\sigma (i)} }[/math] is the [math]\displaystyle{ i }[/math]th largest element in the set [math]\displaystyle{ \left\{ {a_1 , \cdots ,a_n } \right\} }[/math].

Representation theorem of Type-1 OWA operators

Given the n linguistic weights [math]\displaystyle{ \left\{ {W^i} \right\}_{i =1}^n }[/math] in the form of fuzzy sets defined on the domain of discourse [math]\displaystyle{ U = [0,\;\;1] }[/math], and the fuzzy sets [math]\displaystyle{ A^1, \cdots ,A^n }[/math], then we have that

[math]\displaystyle{ Y=G }[/math]

where [math]\displaystyle{ Y }[/math] is the aggregation result obtained by Definition 1, and [math]\displaystyle{ G }[/math] is the result obtained by in Definition 2.

Programming problems for Type-1 OWA operators

According to the Representation Theorem of Type-1 OWA Operators, a general type-1 OWA operator can be decomposed into a series of [math]\displaystyle{ \alpha }[/math]-level type-1 OWA operators. In practice, this series of [math]\displaystyle{ \alpha }[/math]-level type-1 OWA operators is used to construct the resulting aggregation fuzzy set. So we only need to compute the left end-points and right end-points of the intervals [math]\displaystyle{ \Phi _\alpha \left( {A_\alpha ^1 , \cdots ,A_\alpha ^n } \right) }[/math]. Then, the resulting aggregation fuzzy set is constructed with the membership function as follows:

[math]\displaystyle{ \mu _{G} (x) = \operatorname{ \bigvee} \limits_{\alpha :x \in \Phi _\alpha \left( {A_\alpha ^1 , \cdots ,A_\alpha ^n } \right)_\alpha } \alpha }[/math]

For the left end-points, we need to solve the following programming problem:

[math]\displaystyle{ \Phi _\alpha \left( {A_\alpha ^1 , \cdots ,A_\alpha ^n } \right)_{-} = \operatorname {\min }\limits_{\begin{array}{l} W_{\alpha - }^i \le w_i \le W_{\alpha + }^i A_{\alpha - }^i \le a_i \le A_{\alpha + }^i \end{array}} \sum\limits_{i = 1}^n {w_i a_{\sigma (i)} / \sum\limits_{i = 1}^n {w_i } } }[/math]

while for the right end-points, we need to solve the following programming problem:

[math]\displaystyle{ \Phi _\alpha \left( {A_\alpha ^1 , \cdots , A_\alpha ^n } \right)_{+} = \operatorname {\max }\limits_{\begin{array}{l} W_{\alpha - }^i \le w_i \le W_{\alpha + }^i A_{\alpha - }^i \le a_i \le A_{\alpha + }^i \end{array}} \sum\limits_{i = 1}^n {w_i a_{\sigma (i)} / \sum\limits_{i = 1}^n {w_i } } }[/math]

A fast method has been presented to solve two programming problem so that the type-1 OWA aggregation operation can be performed efficiently, for details, please see the paper.

Alpha-level approach to Type-1 OWA operation

Three-step process:

• Step 1—To set up the [math]\displaystyle{ \alpha }[/math]- level resolution in [0, 1].
• Step 2—For each [math]\displaystyle{ \alpha \in [0,1] }[/math],

• Step 2.1—To calculate [math]\displaystyle{ \rho _{\alpha +} ^{i_0^\ast } }[/math]

1. Let [math]\displaystyle{ i_0 = 1 }[/math];
2. If [math]\displaystyle{ \rho _{\alpha +} ^{i_0 } \ge A_{\alpha + }^{\sigma (i_0 )} }[/math], stop, [math]\displaystyle{ \rho _{\alpha +} ^{i_0 } }[/math] is the solution; otherwise go to Step 2.1-3.
3. [math]\displaystyle{ i_0 \leftarrow i_0 + 1 }[/math], go to Step 2.1-2.

• Step 2.2 To calculate[math]\displaystyle{ \rho _{\alpha -} ^{i_0^\ast } }[/math]

1. Let [math]\displaystyle{ i_0 = 1 }[/math];
2. If [math]\displaystyle{ \rho _{\alpha -} ^{i_0 } \ge A_{\alpha - }^{\sigma (i_0 )} }[/math], stop, [math]\displaystyle{ \rho _{\alpha -} ^{i_0 } }[/math] is the solution; otherwise go to Step 2.2-3.
3. [math]\displaystyle{ i_0 \leftarrow i_0 + 1 }[/math], go to step Step 2.2-2.

• Step 3—To construct the aggregation resulting fuzzy set [math]\displaystyle{ G }[/math] based on all the available intervals [math]\displaystyle{ \left[ {\rho _{\alpha -} ^{i_0^\ast } ,\;\rho _{\alpha +} ^{i_0^\ast } } \right] }[/math]:

[math]\displaystyle{ \mu _{G} (x) = \operatorname \bigvee \limits_{\alpha :x \in \left[ {\rho _{\alpha -} ^{i_0^\ast } ,\;\rho _{\alpha +} ^{i_0^\ast } } \right]} \alpha }[/math]

Some Examples

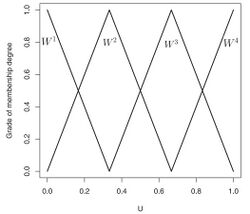
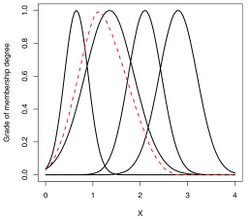
• The type-1 OWA operator with the weights shown in the top figure is used to aggregate the fuzzy sets (solide lines) in the bottom figure, and the dashed line is the aggregation result.

Special cases

• Any OWA operators, like maximum, minimum, mean operators;
• Join operators of (type-1) fuzzy sets, i.e., fuzzy maximum operators;
• Meet operators of (type-1) fuzzy sets, i.e., fuzzy minimum operators;
• Join-like operators of (type-1) fuzzy sets;
• Meet-like operators of (type-1) fuzzy sets.

Generalizations

Type-2 OWA operators have been suggested to aggregate the type-2 fuzzy sets for soft decision making.

Applications

Type-1 OWA operators have been applied to different domains for soft decision making.

• Improved efficiency of computing approach ;
• Type reduction of type-2 fuzzy sets ;
• Group decision making ;
• Credit risk evaluation ;
• Information fusion ;
• Linguistic expressions and symbolic translation ;
• Sentiment analysis ;
• Route selection in uncertain environments ;
• Recommendations on eCommerce .