Uncomputation
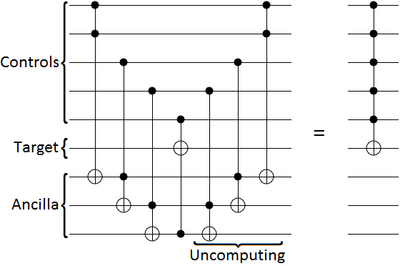
Uncomputation is a technique, used in reversible circuits, for cleaning up temporary effects on ancilla bits so that they can be re-used.[1]
Uncomputation is a fundamental step in quantum computing algorithms. Whether or not intermediate effects have been uncomputed affects how states interfere with each other when measuring results.[2]
The process is primarily motivated by the principle of implicit measurement.[3], which states that discarding a register during computation is physically equivalent to measuring it. Failure to uncompute garbage registers can have unintentional consequences. For example, if we take the state where and are garbage registers. Then, if we do not apply any further operations to those registers, according to the principle of implicit measurement, the entangled state has been measured, resulting in a collapse to either or with probability . What makes this undesirable is that wave-function collapse occurs before the program terminates, and thus may not yield the expected result.
References
- ↑ Aaronson, Scott; Grier, Daniel; Schaeffer, Luke (2015). "The Classification of Reversible Bit Operations". arXiv:1504.05155 [quant-ph].
- ↑ Aaronson, Scott (2002). "Quantum Lower Bound for Recursive Fourier Sampling". Quantum Information and Computation ():, 00 3 (2): 165–174. doi:10.26421/QIC3.2-7. Bibcode: 2002quant.ph..9060A.
- ↑ Nielsen, Michael; Chuang, Isaac. "Quantum Computation and Quantum Information"
 |
